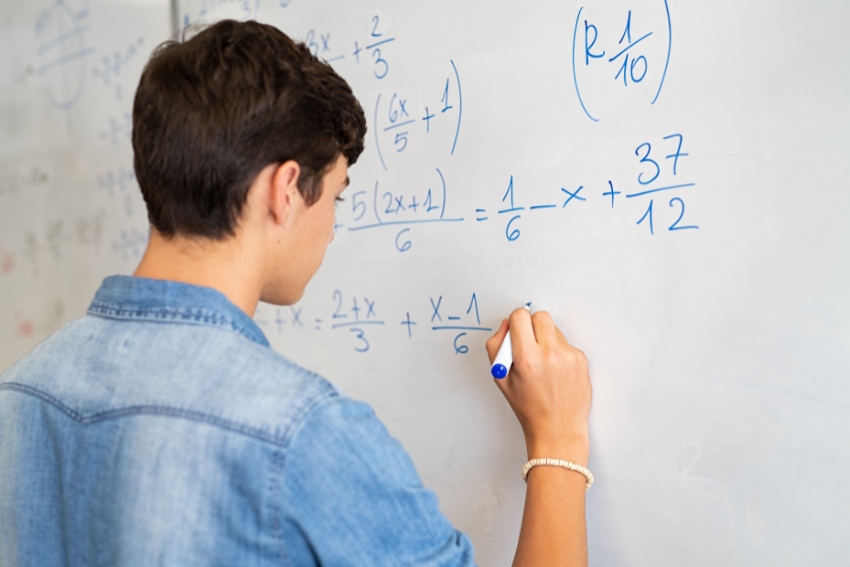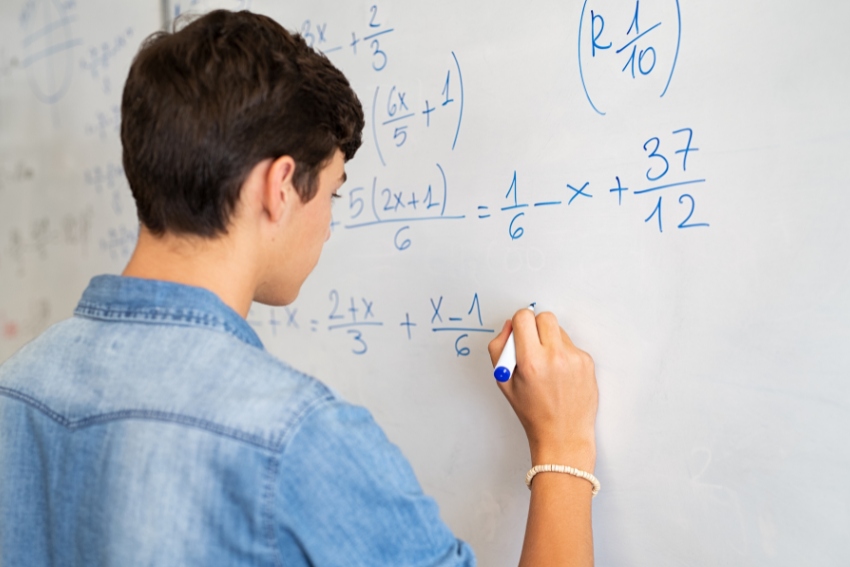Pythagorean Theorem – GCSE Maths – Explained

The Pythagorean theorem might sound like something from a dusty old textbook, but it’s actually a pretty cool concept once you understand. It’s all about figuring out the sides of right-angled triangles, and trust me, it’s easier than you think.

Let’s walk through what the Pythagorean theorem is and why it matters, without making it complicated. We’ll explore how this age-old formula, a² + b² = c², applies not just in your exams but in real-world situations too.

First, Let’s Understand Right-Angled Triangles

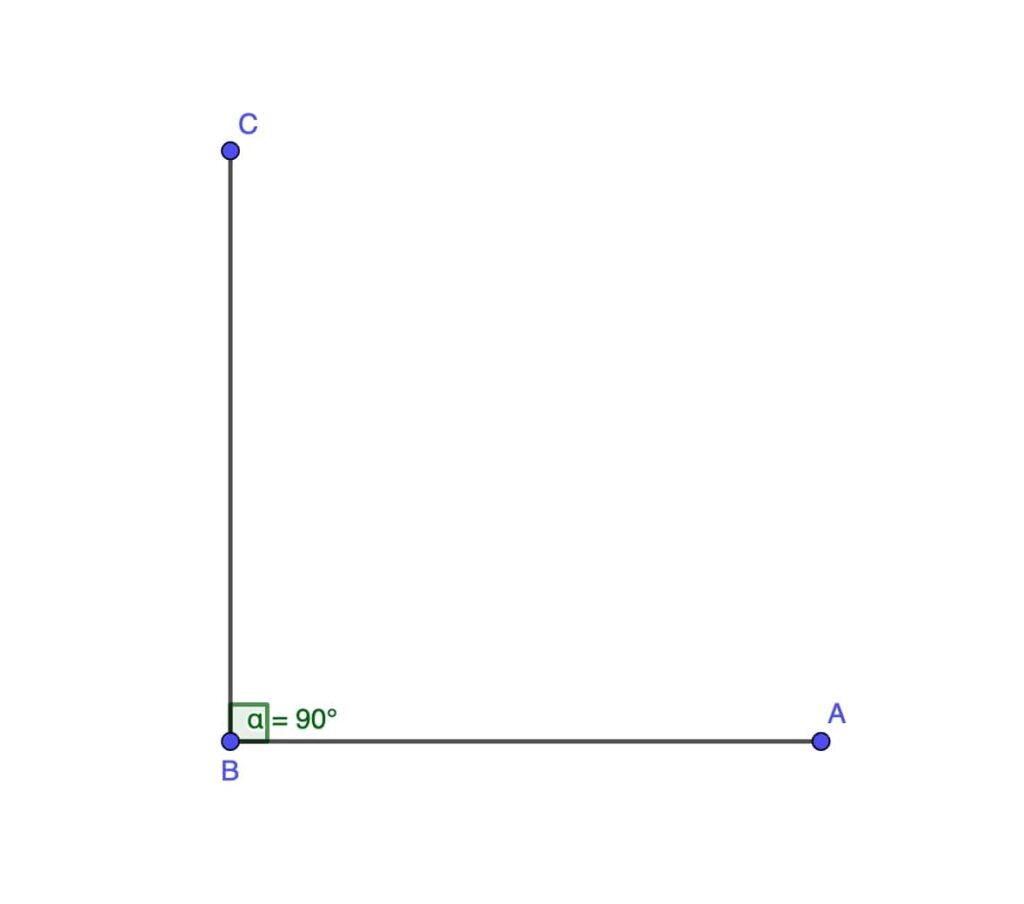
Before explaining the Pythagorean theorem, let’s get our basics clear about right-angled triangles. These special triangles have one angle exactly at 90 degrees, making them a cornerstone in geometry.

Hypotenuse

The hypotenuse is the longest side of the triangle and lies opposite the right angle.

Adjacent Side

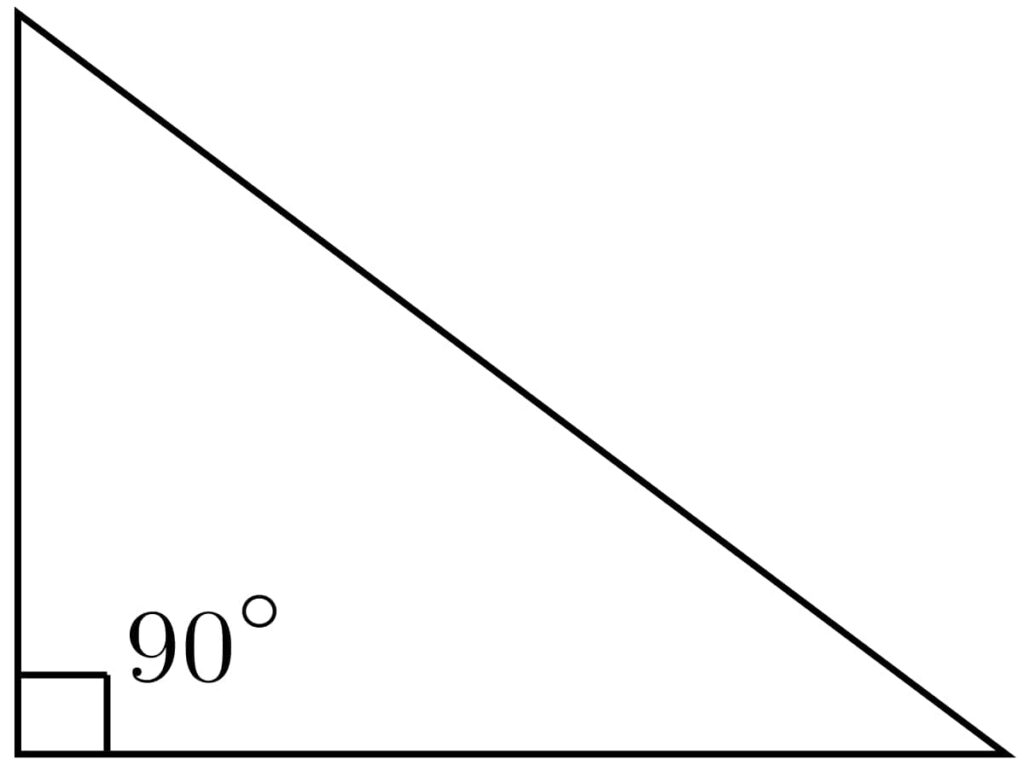
This side is next to the angle you’re focusing on but isn’t the hypotenuse. In a right-angled triangle, it’s one of the sides forming the right angle.

Opposite Side

As the name suggests, it’s directly opposite the angle in question. In right-angled triangles, it’s the side that doesn’t touch the angle you’re looking at (except for the right angle itself).

To make these definitions stick, let’s visualise.

Imagine a ladder leaning against a wall. The ground forms one side of our triangle (adjacent), the wall forms the other (opposite), and the ladder itself? That’s the hypotenuse.

Pythagorean Theorem – Explained

At the heart of our exploration into right-angled triangles lies the Pythagorean theorem. It’s elegantly simple in its formal statement:

a² + b² = c²

Here, (a) and (b) represent the lengths of the triangle’s two shorter sides, while (c) stands for the length of the hypotenuse.

Why It Works

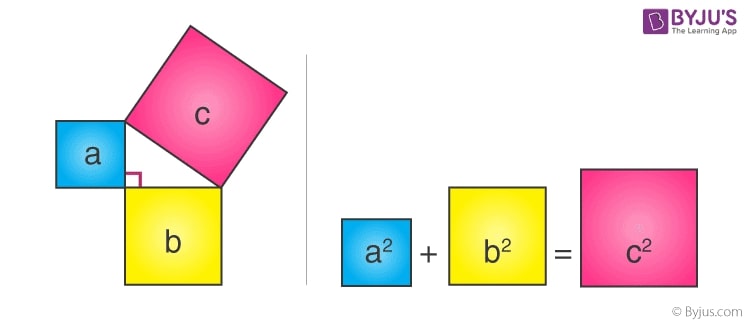
So, why does this theorem hold true? It’s all about the area. Imagine you have three squares, each built on one side of the triangle. The area of the square on the hypotenuse ((c²)) is exactly equal to the sum of the areas of the other two squares ((a² + b²)). This isn’t just a coincidence; it’s a fundamental property of right-angled triangles.

This relationship between the sides means that knowing the lengths of any two sides of a right-angled triangle lets you calculate the third. It’s a tool that mathematicians, architects, and many others have relied on for centuries to understand the world around us. The theorem bridges the abstract (numbers and formulas) with the tangible (physical models and real-world applications), showcasing the harmony between geometry and reality.

The History of Pythagoras Theorem

Pythagoras, a name synonymous with the theorem that bears his name, was more than just a mathematician. He was a philosopher and the leader of a movement with religious and political elements, living around 570-495 BCE in ancient Greece. His life is shrouded in mystery and legend, making him a fascinating historical figure.

The Historical Evolution of the Theorem

Although the theorem is named after Pythagoras, evidence suggests that the Babylonians and Indians understood the relationship between the sides of a right-angled triangle centuries before him. However, Pythagoras is credited with proving the theorem, thereby establishing a fundamental principle of geometry.

Over the centuries, the Pythagorean theorem has evolved not just as a mathematical principle but as a symbol of intellectual achievement and the power of deductive reasoning. It has been proved in numerous ways by mathematicians across different cultures, showcasing its universal truth beyond the confines of any single civilization. This historical journey highlights the theorem’s significance as a cornerstone of mathematics and its enduring legacy that continues to inspire curiosity and discovery.

The Formula of Pythagorean Theorem and Its Proof

Understanding the Pythagorean theorem starts with its formula: (a² + b² = c²). This formula tells us that in a right-angled triangle, the square of the hypotenuse ((c)) is equal to the sum of the squares of the other two sides ((a) and (b)). But how do we arrive at this conclusion? Let’s break it down.

Step-by-Step Derivation

1. Start with a right-angled triangle. Label the sides opposite and adjacent to the right angle as (a) and (b), and the hypotenuse as (c).
2. Construct squares on each side of the triangle. You’ll have one square for each side, so three in total.
3. Use area to understand the relationship. The area of the square built on the hypotenuse ((c²)) can be shown to be equal to the sum of the areas of the other two squares ((a² + b²)). This is because the space can be rearranged without changing the total area, aligning with the principle of conservation of area in geometry.

Simple Proof for GCSE Students

One of the simplest proofs involves using two identical right-angled triangles to form a square. Here’s a basic overview:

1. Create a large square by placing four identical right-angled triangles together. The sides (a) and (b) form the inner square, and (c) becomes the side of the larger square.
2. Calculate the area of the large square two ways: by its sides ((c²)) and by the sum of the area of the inner square ((a² + b²)) plus the area of the four triangles.
3. Observe that both methods should give the same total area for the large square, leading to the conclusion that (a² + b² = c²).

This proof doesn’t require advanced mathematics but a logical approach to the arrangement and properties of shapes, making it accessible and understandable for students at the GCSE level.

Various Proofs and Perspectives

The beauty of the Pythagorean theorem lies not just in its simplicity but in the myriad ways it can be proved, each offering a unique perspective. These proofs, ranging from geometric to algebraic, underscore the theorem’s versatility and its foundational role in mathematics.

Geometric Proofs

Geometric proofs rely on shapes, areas, and visual manipulations to demonstrate the theorem’s truth. One popular geometric proof involves rearranging triangles and squares to show that the areas match up, much like a puzzle. Another involves drawing similar triangles within the original right-angled triangle, using the properties of these similar triangles to prove the theorem. These visual strategies not only prove the theorem but also deepen our understanding of geometric principles.

Algebraic Proofs

Algebraic proofs, on the other hand, use equations and algebraic manipulations. These proofs might start with the areas of squares built on the sides of a right-angled triangle, expressing these areas in terms of (a), (b), and (c), and then using algebra to show that (a² + b² = c²). Algebraic proofs highlight the numerical relationships between the sides of the triangle and provide a clear, step-by-step logical argument for the theorem.

Will You Ever Use Pythagorean Theorem in Real Life?

The Pythagorean theorem isn’t just a staple of geometry textbooks; it’s a tool that’s used in numerous real-world scenarios. From architecture to navigation, this ancient theorem has modern-day applications that might surprise you.

Practical Examples

• Architecture and Construction: Architects and construction workers use the Pythagorean theorem to ensure buildings are level and to calculate the correct slope of roofs and staircases. For example, to determine the length of the ladder needed to reach a certain height while ensuring stability, the theorem comes into play.
• Navigation: Sailors and pilots often rely on the Pythagorean theorem for charting courses. By considering the earth’s surface as a series of right-angled triangles, they can calculate the shortest distance between two points, crucial for efficient and safe travel.
• Everyday Scenarios: Ever wonder if that large furniture piece will fit through your door or up your stairway? The Pythagorean theorem can help you figure it out without having to lift a finger (well, maybe just for some measuring).

Exercises for Students

1. Building a Treehouse: Calculate the height of a tree where you plan to build a treehouse if you know the distance from the tree’s base to a point on the ground and the length of the ladder you’ll lean against the tree.
2. Planning a Path: Imagine you want to create a straight path in your backyard from the corner of your house to the opposite end of your yard. How can you use the Pythagorean theorem to ensure the path is direct and save on materials?
3. Home DIY Project: You’re designing a rectangular garden bed that needs to fit in a specific area of your yard. If you know the length and width of the garden bed, how can you use the Pythagorean theorem to ensure the corners are right angles?

These exercises encourage students to apply the Pythagorean theorem in practical situations, demonstrating its value beyond the classroom and fostering a deeper appreciation for mathematics in everyday life.

Conclusion

It’s clear Pythagorean theorem isn’t just a relic of the past. Its applications in today’s world, from the simplicity of home projects to the complexities of navigation, demonstrate its enduring relevance. Mathematics, with tools like this, serves as a bridge connecting theoretical knowledge with practical solutions, proving that ancient wisdom can solve modern problems.

For students aiming to master not just the Pythagorean theorem but all aspects of GCSE maths, seeking the right guidance is crucial. Edumentors, an online tutoring platform, offers access to top UK tutors who aren’t just academically accomplished but are also navigating the same journey at top UK universities. This unique opportunity allows students to learn from those who have successfully traversed the path to academic excellence, offering insights, tips, and personalised coaching to help achieve those desired grades and potentially open doors to top UK universities. With Edumentors, the journey through mathematics becomes not just about passing exams but about laying a solid foundation for future success.