Angles in Maths – Angles Explained – GCSE Maths Revision

Angles are a vital component of GCSE maths.

At first glance, angles might seem straightforward, but a deeper understanding of their properties and the various types of angles can significantly enhance your mathematical skills and help you score a 9.

This blog goes into detail about angles, from the basic definitions to the complex rules that govern their behaviour.

What are Angles?

An angle in mathematics is formed when two lines intersect or meet at a point, known as the vertex. The amount of turn between each arm of the angle is what defines its size. Angles are more than just geometric figures; they are a fundamental aspect of mathematics, influencing various fields such as architecture, engineering, and even art.

Angles are typically measured in degrees, a unit that helps quantify the size of an angle. A full circle encompasses 360 degrees, dividing the circular path into equal parts. Understanding degrees is crucial in calculating and comprehending the precise dimensions of an angle. This measurement system allows for accurate representation and manipulation of angles in both theoretical and practical applications in mathematics and beyond.

What are Different Angle Types?

Exploring the variety of angles is crucial for understanding their role in mathematics and geometry. Here are the main types of angles you’ll encounter:

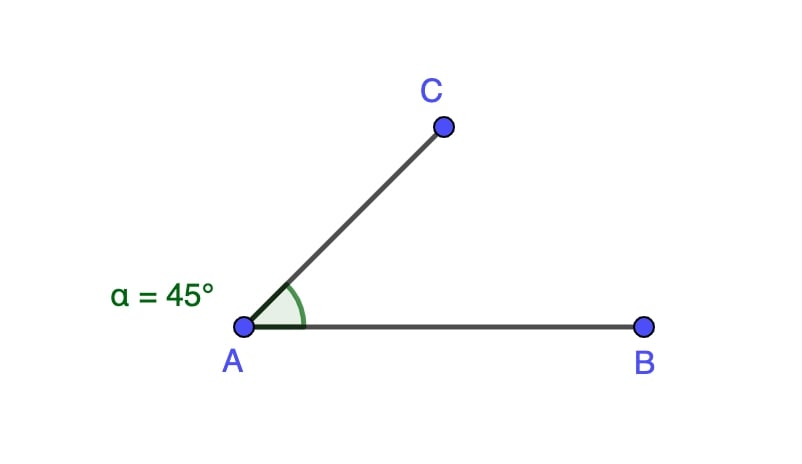
An acute angle is smaller than 90 degrees. It’s a sharp angle, often found in various geometric figures and everyday objects.

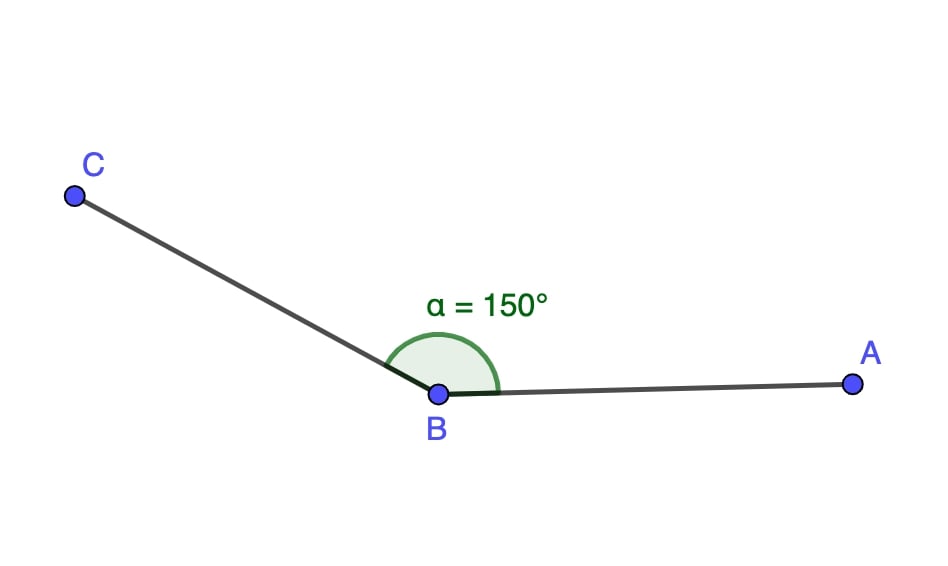
An obtuse angle is larger than 90 degrees but less than 180 degrees. It appears more spread out than an acute angle and is commonly seen in real-world structures.

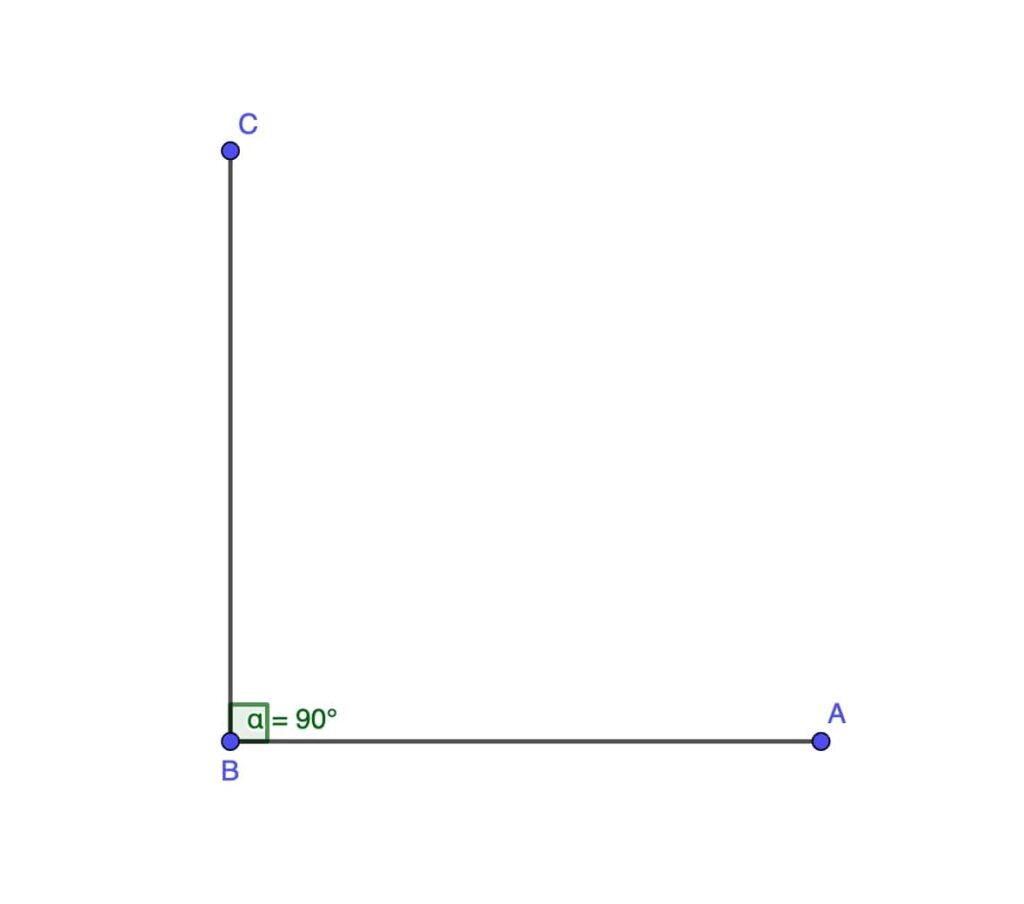
A right angle is exactly 90 degrees and is one of the most familiar types of angles, often associated with the corners of squares and rectangles.

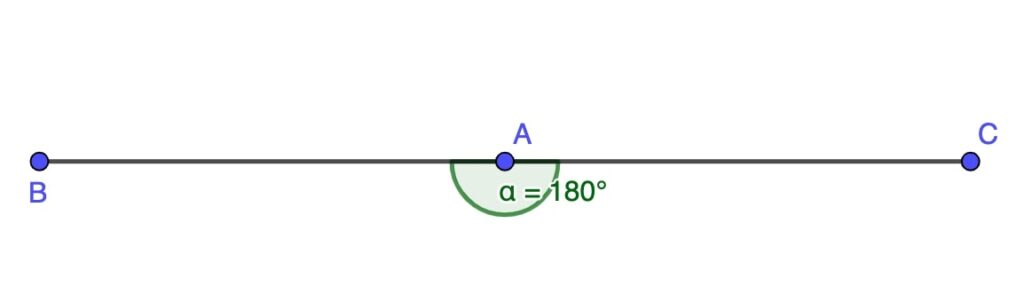
A straight angle is 180 degrees and looks like a straight line. This type of angle represents a half turn and is pivotal in geometry.

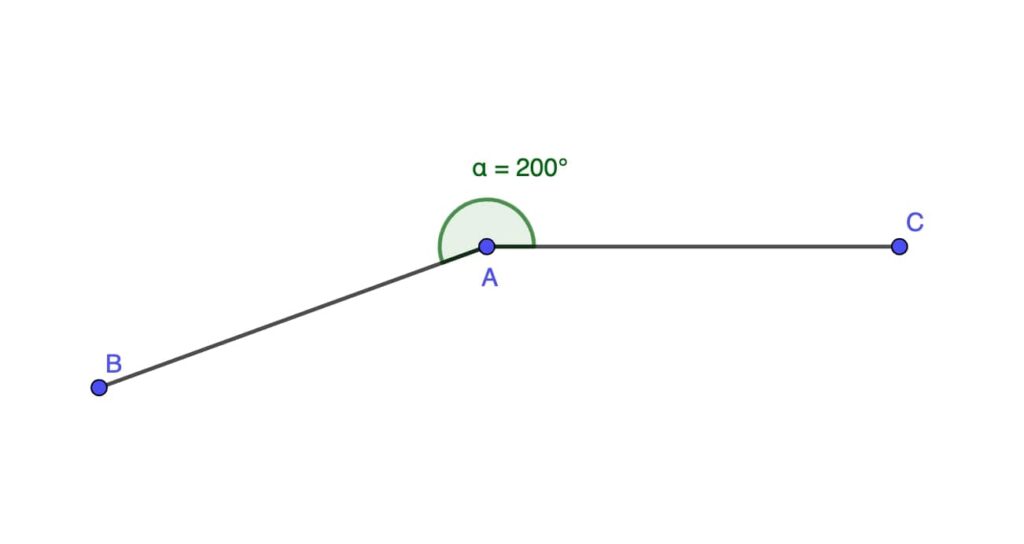
A reflex angle is more than 180 degrees but less than 360 degrees. It’s larger than a straight angle and is less commonly encountered in everyday geometry.

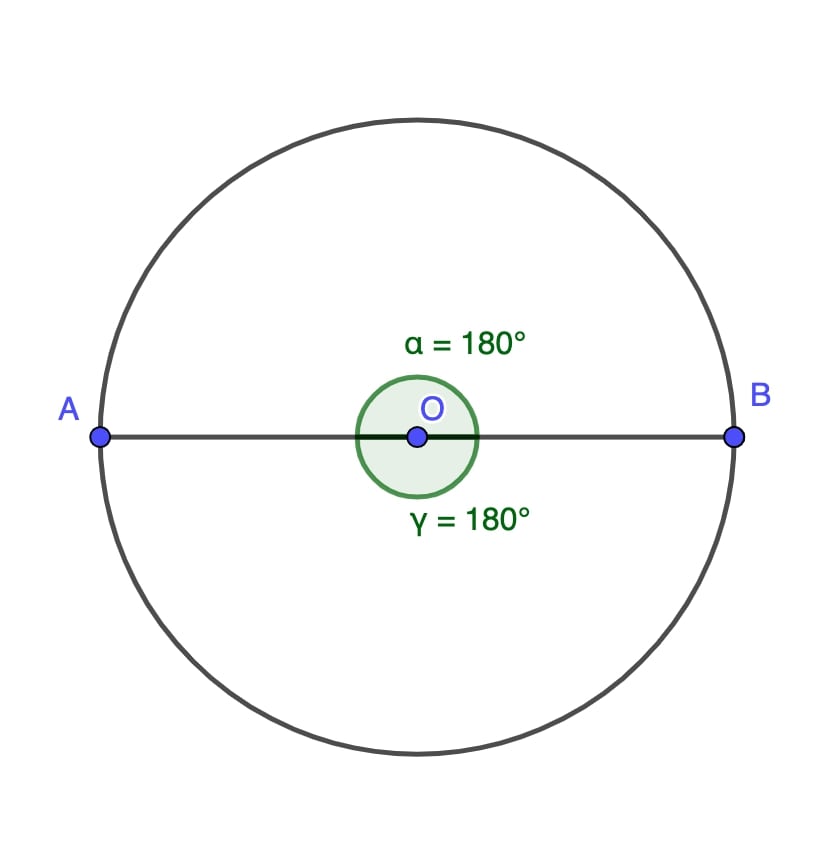
A full rotation angle is exactly 360 degrees, representing a complete circle. It’s essential in understanding circular motion and geometry.

Angle Rules and Properties

Understanding the fundamental facts, rules, and properties of angles is essential for anyone studying geometry, especially at the GCSE level. Let’s explore some of these key concepts:

Fundamental Angle Facts and Rules

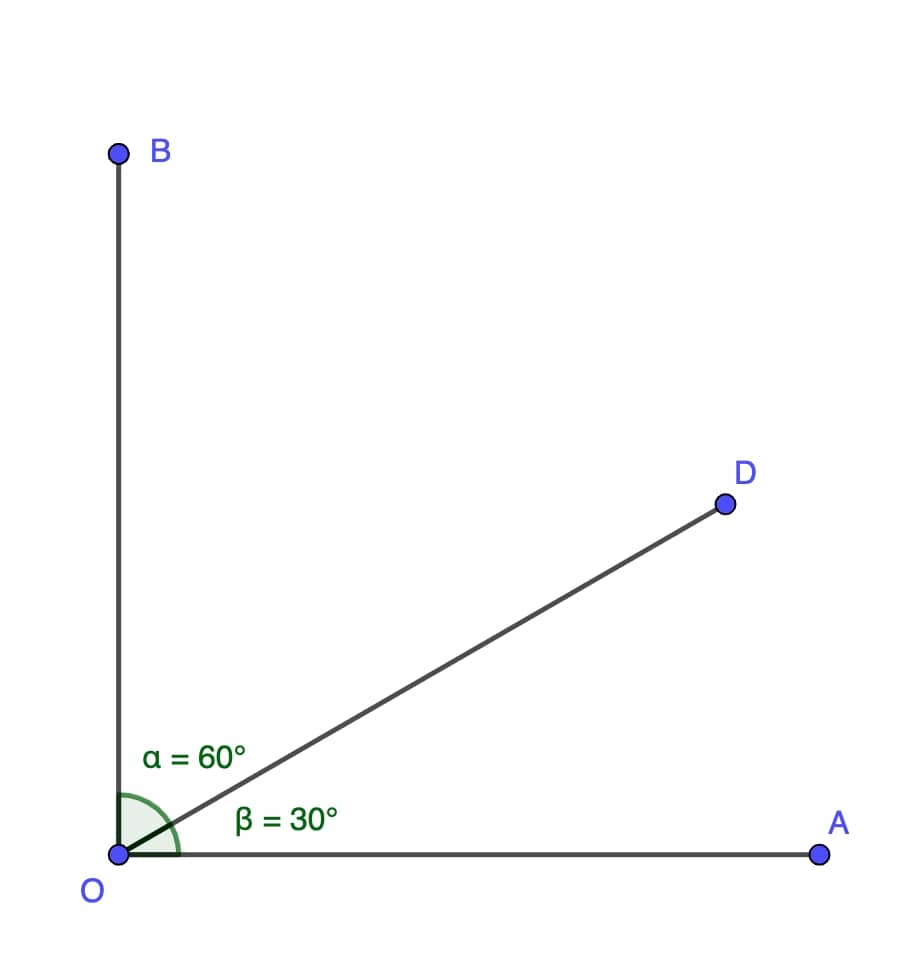
Two angles are complementary if their sum is 90 degrees. These often appear in various geometric shapes and real-world contexts.

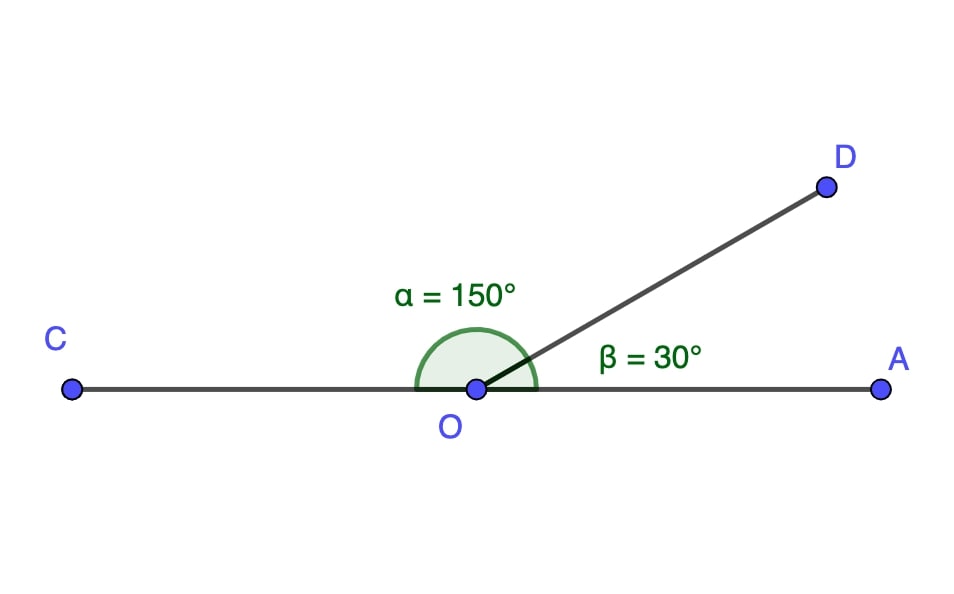
Two angles are supplementary when they add up to 180 degrees. They are frequently observed in geometric constructions and design.

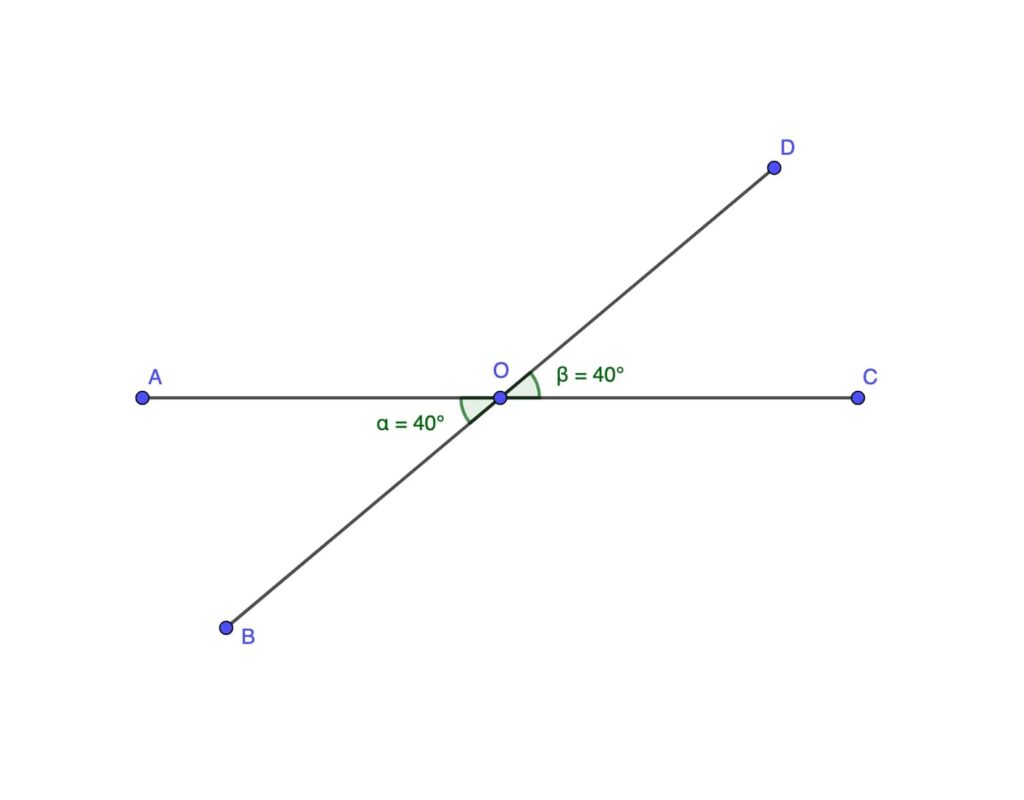
When two lines intersect, the opposite angles formed are equal. This rule is a cornerstone in geometry and is pivotal in many proofs and problems.

Properties of Angles

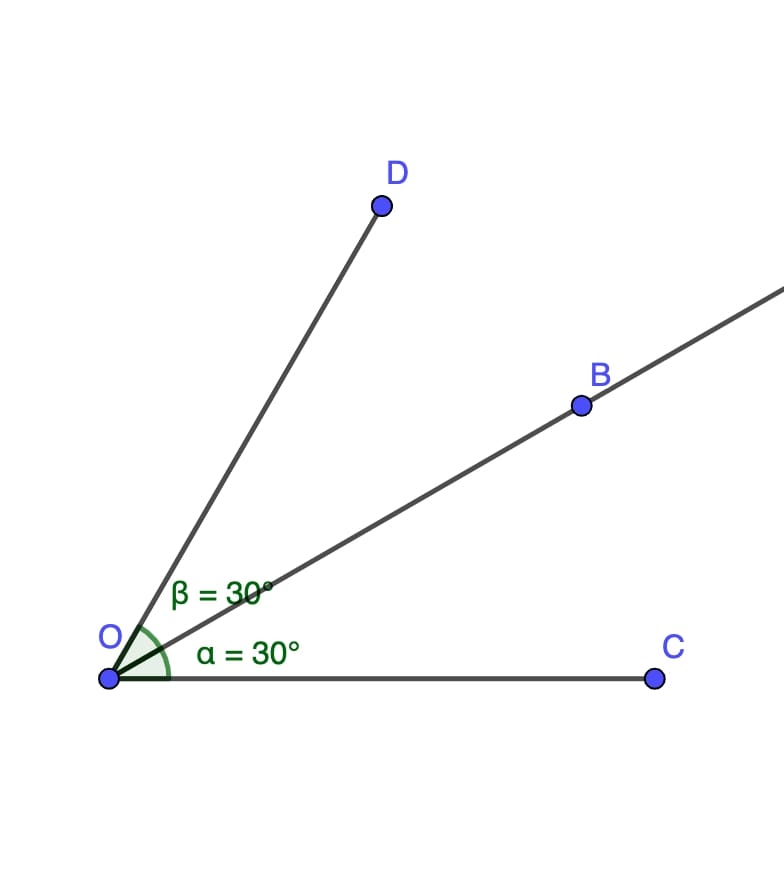
A line that divides an angle into two equal parts. It’s a common concept in both theoretical geometry and practical applications.

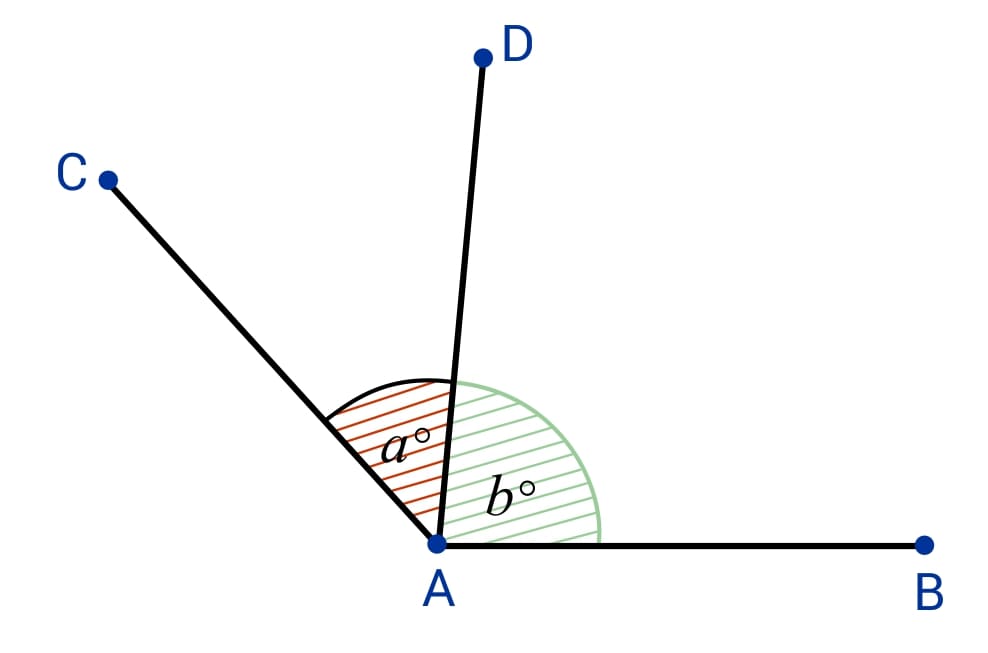
Angles that share a common side and vertex. Understanding their relationships is crucial in solving many geometric problems.

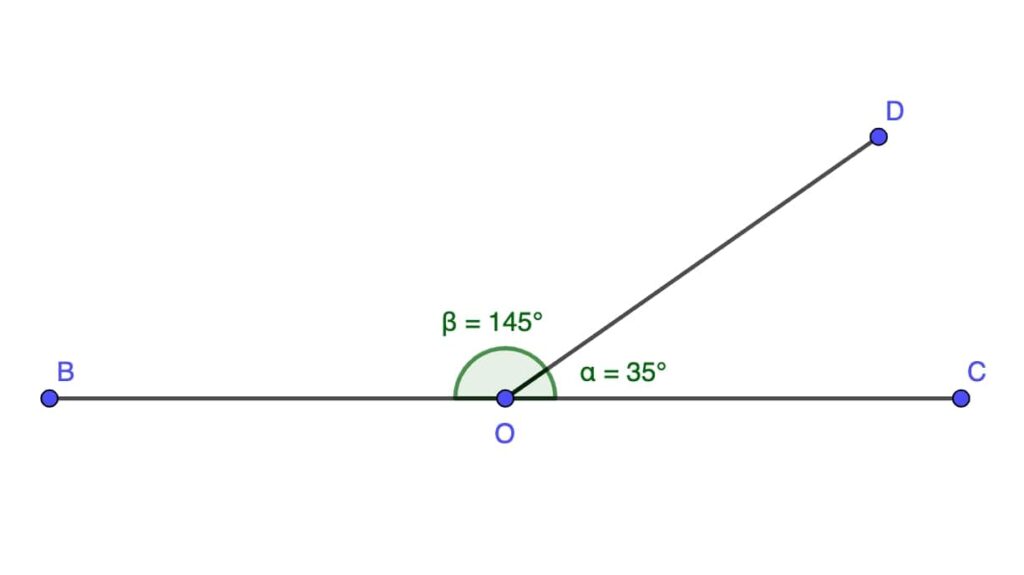
A pair of adjacent angles whose non-common sides form a straight line. The sum of these angles is always 180 degrees.

Angles in Polygons

Polygons, which are shapes with three or more straight sides, have intriguing angle properties. A deeper understanding of these angles is vital for mastering geometry, particularly in GCSE maths.

Understanding Interior and Exterior Angles in Polygons

Interior Angles

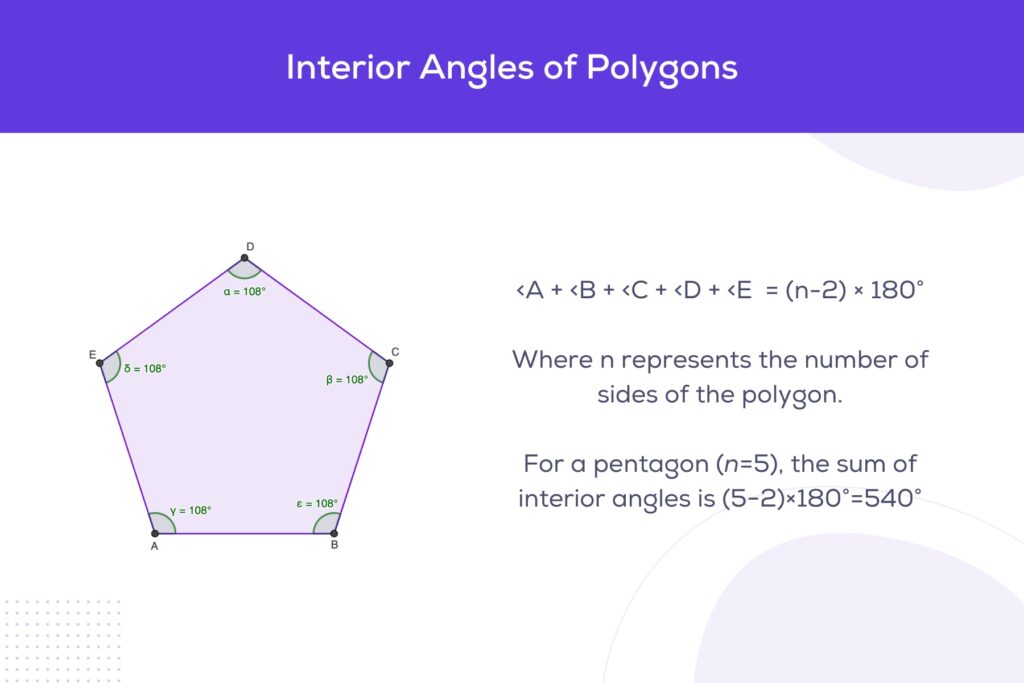
These are the angles found inside the polygon. For any polygon, the sum of the interior angles can be determined by the formula (n-2) × 180°, where ‘n’ is the number of sides. This formula is pivotal in solving many geometric problems involving polygons.

• In a triangle, the sum of the interior angles is always 180 degrees, a key fact in triangle geometry.
• For quadrilaterals, the sum of the interior angles is 360 degrees, reflecting their four-sided nature.
• In regular polygons, where all sides and angles are equal, each interior angle can be found using the formula for the sum of interior angles divided by the number of angles, providing a straightforward way to calculate individual angles.
• For irregular polygons, where sides and angles are not equal, the sum of interior angles still follows the general formula, but calculating individual angles may require additional geometric principles or information.

Exterior Angles

The exterior angles are formed by extending one side of the polygon at each vertex. Interestingly, no matter how many sides a polygon has, the sum of its exterior angles always equals 360 degrees. This constant sum is a fundamental concept in polygon geometry and is particularly useful in various mathematical proofs and constructions.

Angles in Parallel Lines

When a pair of parallel lines is crossed by another line, known as a transversal, several angles are formed. These angles have specific names and properties based on their positions relative to the parallel lines and the transversal.

Corresponding Angles

These angles are located in matching corners when the transversal crosses the parallel lines. They are equal in measure. For example, if one corresponding angle measures 60 degrees, the other corresponding angle will also measure 60 degrees.

Alternate Angles

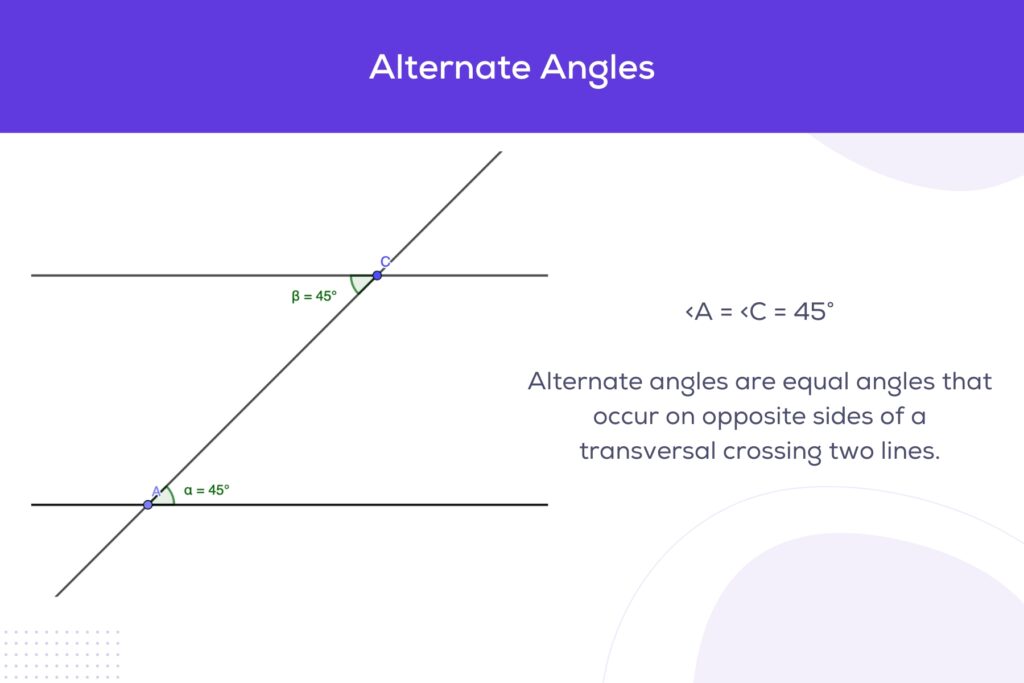
Also known as ‘Z angles’ due to the Z-shape formed when looking at them, alternate angles are equal. They are found on opposite sides of the transversal but inside the parallel lines. Alternate angles are a crucial concept in proofs and problem-solving involving parallel lines.

Co-Interior Angles

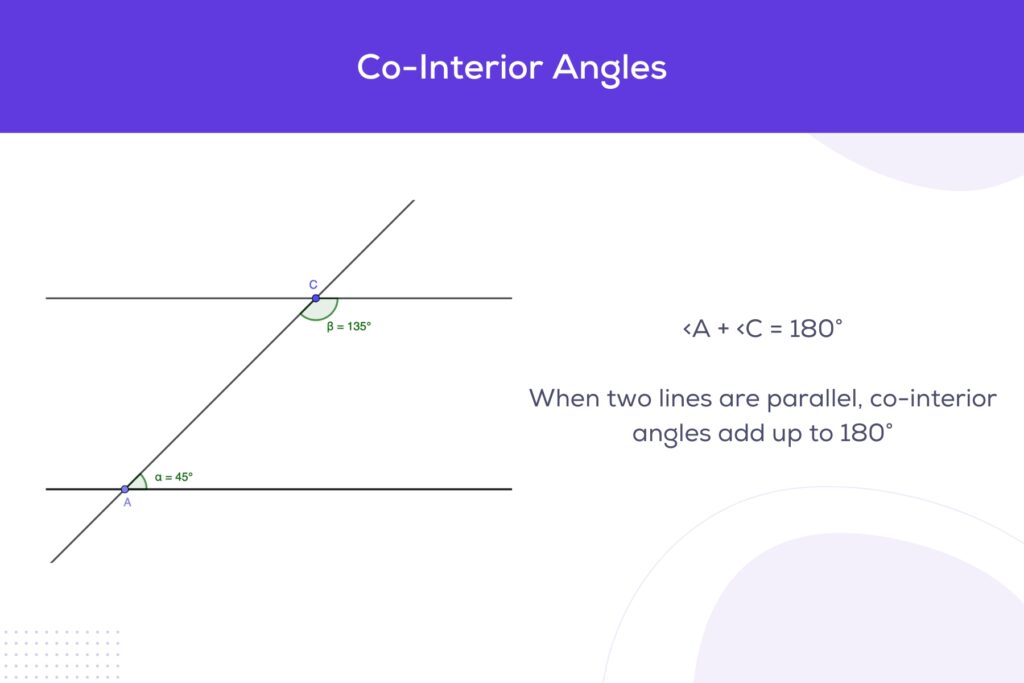
These angles, sometimes referred to as ‘C angles’ due to the C-shape formed, are on the same side of the transversal and inside the parallel lines. The sum of co-interior angles is always 180 degrees. This property is particularly useful in determining unknown angle measures and in various geometric constructions.

Measuring and Constructing Angles

Accurately measuring and constructing angles is a fundamental skill in geometry, especially for students preparing for GCSE maths. The protractor, a common mathematical tool, is indispensable in this process. Let’s explore how to effectively use a protractor and provide step-by-step instructions for constructing common angles.

How to Use a Protractor?

Using a protractor properly is crucial for measuring angles accurately. Here’s how you can use it:

1. Place the protractor so that the midpoint of its straight edge aligns with the vertex of the angle you are measuring.
2. Ensure that the base line of the protractor (the ‘0’ line) is exactly along one arm of the angle.
3. Look where the other arm of the angle intersects the numbered scale on the protractor. The protractor has two sets of numbers; use the set that starts from the base line of the angle. This number is the measure of the angle in degrees.
4. To draw an angle, start by drawing one arm. Place the protractor’s midpoint at the end of this arm and mark a dot at the degree measurement you desire. Then, remove the protractor and draw a line from the vertex to the marked dot.

Step-by-Step Instructions for Constructing Common Angles

• Constructing a 60-Degree Angle
  1. Draw a straight line (base line).
  2. Using a protractor, place the midpoint on one end of the line.
  3. Mark a point at 60 degrees on the protractor.
  4. Remove the protractor and draw a line from the endpoint of the base line to the marked point.
• Constructing a 90-Degree (Right) Angle
  1. Draw a straight line.
  2. Align the protractor’s midpoint and base line as described above.
  3. Mark a point at 90 degrees.
  4. Draw a line from the base line’s endpoint to the 90-degree mark.
• Constructing a 45-Degree Angle
  1. Follow the same steps, but mark a point at 45 degrees on the protractor.
  2. Draw the line from the base line’s endpoint to the 45-degree mark.

Conclusion

In this comprehensive exploration, we’ve journeyed through the multifaceted world of angles, a cornerstone of geometry and an essential component of GCSE maths. From the basic understanding of what angles are and their measurement in degrees to the complexities of their types, properties, and roles in polygons and parallel lines, we’ve covered substantial ground. Moreover, we delved into the practical aspects of using a protractor for measuring and constructing angles, equipping you with the tools needed to master this crucial mathematical concept.

As you prepare for your GCSE maths exams, remember that understanding these concepts is about more than memorisation—it’s about developing a clear comprehension and an ability to apply these principles in various problems. Regular practice, combined with a focus on problem-solving and conceptual clarity, is key to excelling in maths. If you find certain areas challenging, don’t hesitate to seek guidance. Working with a GCSE maths tutor can provide personalised support, helping to clarify doubts and strengthen your understanding in areas where you might struggle. Remember, maths is a subject best mastered through practice, patience, and persistence. So, keep exploring, practicing, and don’t be afraid to ask for help when needed.