Sin, Cos and Tan is an important concept in trigonometry, which you will need to familiarise with to have a deeper understanding of concepts in GCSE exams. To create a simplified and more accessible guide to understanding sine (sin), cosine (cos), and tangent (tan), , let’s break down each part of your request following the provided outline.
What are Sin, Cos, and Tan?
Sin, Cos, and Tan are trigonometric functions that relate the angles of a right-angled triangle to the lengths of its sides. Each function serves a unique purpose in calculating the dimensions of a triangle when certain other aspects of the triangle are known.
- Sine (sin) of an angle in a right-angled triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos) is the ratio of the length of the adjacent side to the angle to the hypotenuse.
- Tangent (tan) is the ratio of the opposite side to the adjacent side.
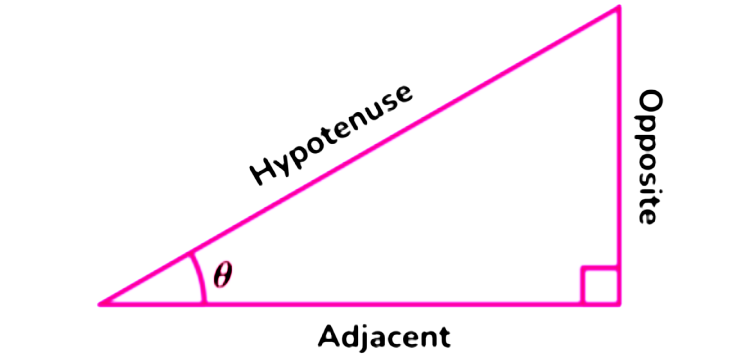
- θ is the angle.
- The opposite side (O)(O) is opposite to the angle.
- The adjacent side (A)(A) is next to the angle.
- The hypotenuse (H)(H) is the longest side.
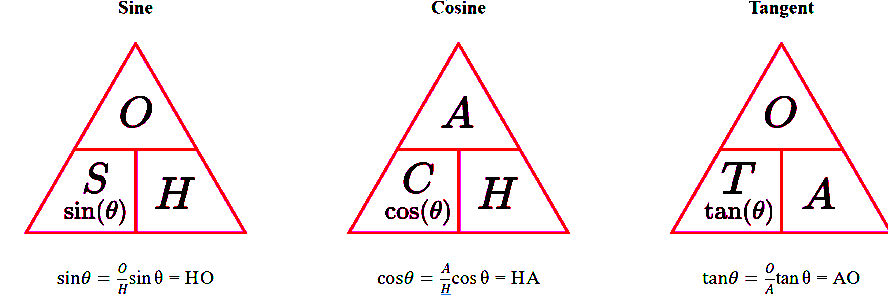
SOHCAHTOA – Trigonometric Formulae
SOHCAHTOA is a mnemonic that helps remember the trigonometric formulae:
- Sine = Opposite / Hypotenuse
- Cosine = Adjacent / Hypotenuse
- Tangent = Opposite / Adjacent
These three trigonometric ratios are used to determine a missing side or a missing angle. Here is a visual representation:
How to Calculate Using Sin, Cos, Tan
Calculating angles or sides using sin, cos, and tan involves rearranging the formulas to solve for the unknown. For example, if you know the lengths of the opposite side and the hypotenuse, you can calculate the angle using the sine function:
- Identify the known sides of the triangle in relation to the angle you’re interested in.
- Choose the appropriate trigonometric function based on the sides you know (SOH for sin, CAH for cos, TOA for tan).
- Rearrange the formula if necessary to solve for the unknown (side length or angle).
- Use a calculator to compute the angle (using the inverse functions sin⁻¹, cos⁻¹, tan⁻¹) or the length of the side.
For angles, remember to set your calculator to the correct unit (degrees or radians) based on the context of the problem.
Why Knowing Sin, Cos, Tan is Important for the GCSE Exam
Understanding sin, cos, and tan is crucial for GCSE Maths exams as these concepts form the foundation of trigonometry, a significant part of the syllabus. Mastery of these trigonometric functions enables students to solve a wide range of problems, from calculating angles and sides of triangles to applying these concepts in real-world contexts, such as engineering, physics, and geography.
Knowing how to use these functions effectively can also help in understanding more complex mathematical concepts, improving spatial reasoning, and developing problem-solving skills. Therefore, investing time to grasp these fundamental trigonometric relationships can significantly enhance a student’s mathematical capability and confidence in tackling exam questions involving trigonometry.
What can Help?
If you feel discouraged or overwhelmed by what lays ahead of you, GCSE maths tutors might be able to help. These student-tutors from UK’s top universities can not only give you academic knowledge but also relate to you in ways others might not be able to.