Exams & Revisions - Parents Exams & Revisions - Students GCSEs - Parents GCSEs - Students

GCSE Maths – Numbers

Tornike Asatiani July 22, 2023

Number Structure and Calculation

Number Structure and Calculation forms the bedrock of mathematics. It’s all about understanding the different types of numbers that exist, how they are related, and how we can manipulate them through various calculations. Let’s break it down.

Different Types of Numbers

Just like the way we have different categories of living beings – mammals, birds, insects, fish, etc., in the world of maths, we categorise numbers too!

Natural Numbers

The very first type of numbers that we come across are the Natural Numbers. They are the counting numbers that we use every day: 1, 2, 3, 4, 5, and so on. Suppose you’re counting the number of books on your shelf or the number of cookies in a jar, you’re dealing with natural numbers!

Whole Numbers

Then we have the Whole Numbers, which are just like natural numbers, but with the addition of 0. Why add zero? Imagine you’re at a concert, and they’re counting down the time to the start. The countdown goes 3, 2, 1 and then…0! The concert begins.

Integers

Next up are the Integers, which include positive natural numbers, zero, and also negative numbers. Imagine you’re playing a video game where you can gain or lose points. Your score could be +3 if you gained points, 0 if you’re just starting, or -3 if you lost some.

Rational and Irrational Numbers

Following that, we encounter the Rational and Irrational numbers. Rational numbers are simply numbers that can be expressed as fractions (like 1/2, -3/4, 5). And irrational numbers, on the other hand, are numbers that can’t be written as a simple fraction, like the value of pi (∏), which has a never-ending and never-repeating decimal value.

Real Numbers

Lastly, the Real Numbers, the broadest category of all, encompass all the numbers we’ve mentioned so far: natural, whole, integers, rational, and irrational numbers.

The Art of Calculation

Now, let’s talk about how we use these numbers. When we perform operations on these numbers, such as addition, subtraction, multiplication, and division, we’re carrying out what’s called ‘calculation.’

Arithmetic Operations

The basic operations are addition, subtraction, multiplication, and division.

For example, if you have five apples and your friend gives you three more, you have 5 (your apples) + 3 (your friend's apples) = 8 apples. That’s addition! Subtraction could be eating two of those apples, multiplication could be buying three times as many, and division could be sharing your apples evenly between friends.

Order of Operations

It’s important to note that these operations have a certain order, commonly remembered with the acronym BIDMAS or BODMAS, which stands for Brackets, Indices (or Orders, meaning powers or roots), Division and Multiplication (from left to right), Addition and Subtraction (from left to right). This order of operations helps avoid any confusion when calculating. For example, for a calculation like 3 + 2 * 4, you should do the multiplication before the addition, giving you 3 + 8 = 11, not 5 * 4 = 20.

Working with Positives and Negatives

Working with positive and negative numbers also has its own set of rules. For example, if you’re feeling warm (let’s call this a positive feeling) and then you eat a chilli pepper (+ hot), you’ll feel even warmer: + (warm) + (+ hot) = + (hotter). On the other hand, if you’re feeling warm and you drink a cold milkshake (- cold), you’ll feel less warm: + (warm) - (- cold) = less warm.

Exponents and Roots

Finally, we have exponents (or powers) and roots. An exponent tells us how many times to multiply a number by itself. For example, 2^3 means 2 * 2 * 2 = 8. Roots are the opposite of exponents. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 * 3 = 9.

Mastering number structure and calculation is a bit like learning the grammar of the language of mathematics. It may seem complicated at first, but with practice, it will become second nature and it will be an invaluable tool for solving more complex problems later on!

Fractions, Decimals, and Percentages

The world of maths is not always about whole numbers. Sometimes, you need to express quantities that are less than one, or you need to compare quantities in different ways. This is where fractions, decimals, and percentages come into play.

Fractions /

Imagine you are at a birthday party and there’s a delicious pizza on the table. But, you can’t have the whole pizza to yourself, you need to share it with your friends. This situation is perfectly described using fractions!

A fraction is a way of expressing a quantity that is less than one, or between two whole numbers. It’s written as two numbers separated by a slash, like 1/2, 3/4, or 5/8. The top number, called the numerator, represents how many parts we have. The bottom number, the denominator, tells us how many equal parts the whole is divided into.

So if you eat 2 slices out of an 8-slice pizza, you would have eaten 2/8 (or simplified to 1/4) of the pizza.

Decimals ,

Now, let’s think about money. If you have half a dollar, we usually express this as $0.50 rather than 1/2 of a dollar. This is a decimal representation.

A decimal number is another way to express fractions, but it does so based on powers of ten. The value of each digit in a decimal number depends on its position relative to the decimal point. For example, in the number 18.273, the digit 1 is in the ‘tens’ place, 8 is in the ‘ones’ place, 2 is in the ‘tenths’ place, 7 is in the ‘hundredths’ place, and 3 is in the ‘thousandths’ place.

Kora F.

Maths | Chemistry | Biology Tutor

Student at UNIVERSITY OF LEEDS

£17 Per session

Book Free Trial

Percentages %

Last but not least, let’s discuss percentages. If you’ve ever gone shopping and seen a sign that says “50% off”, you have encountered a percentage!

A percentage is a way of expressing a number as a fraction of 100. It’s very useful for comparing quantities. In the example above, “50% off” means that the price has been reduced by 50 parts out of a total of 100, or half the original price.

Converting between fractions, decimals, and percentages is a common task in maths. For example, the fraction 1/2 is equivalent to the decimal 0.5, which is also the same as 50%.

These are different tools in your mathematical toolkit, and being fluent in all three will allow you to solve a variety of problems. Whether you’re calculating discounts, measuring ingredients for a recipe, or interpreting data, fractions, decimals, and percentages are everywhere.

Measures and Accuracy

In the real world, everything we measure is subject to some degree of uncertainty or error. Whether we’re baking a cake, building a bookshelf, or conducting a scientific experiment, it’s crucial to understand the concepts of measures and accuracy.

Units and Measurement

Measurements help us understand the world around us. When we talk about how tall someone is, how hot a cup of tea is, or how far away a town is, we’re using measurements.

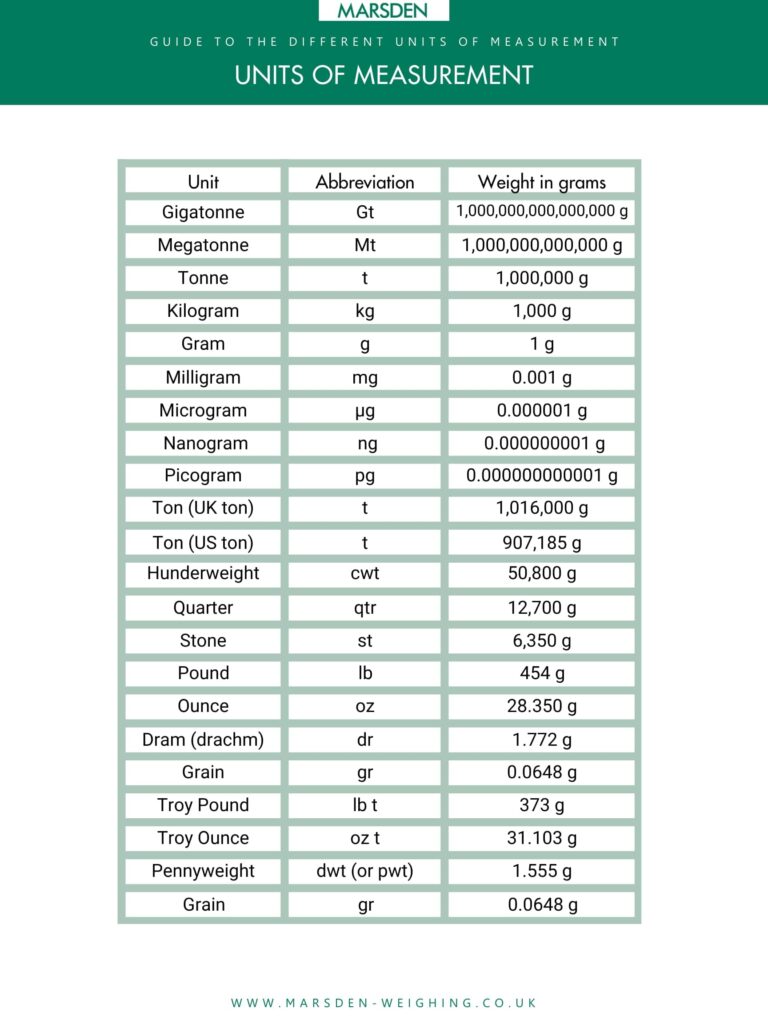
Measurements come in various types, each with their own units. Length could be measured in millimetres, centimetres, metres, kilometres, inches, feet, yards or miles. Volume could be measured in millilitres, litres, cubic centimetres, cubic metres, teaspoons, tablespoons, cups, pints, quarts or gallons. Weight might be in milligrams, grams, kilograms, tonnes, ounces, pounds or stones. Temperature might be in degrees Celsius, degrees Fahrenheit or kelvin.

Each measurement type and unit is best suited to specific contexts, and being able to convert between units is a key skill. For example, knowing that 1 kilometre equals 1000 metres can help when planning a jogging route.

Precision and Accuracy

Precision and accuracy are two terms that often come up when discussing measurements.

Accuracy refers to how close a measured value is to the actual (true) value. If you measure the length of a table with a ruler and get 2 metres, your measurement is said to be accurate if the table’s actual length is indeed 2 metres.

Precision, on the other hand, refers to how close the measurements are to each other. If you measure the same table several times and get 2 metres every time, your measurements are precise.

Ideally, we want our measurements to be both accurate (close to the true value) and precise (values close to each other).

Rounding and Significant Figures

When working with measurements, we often have to deal with more digits than we actually need. This is where rounding becomes useful. It helps us simplify numbers without significantly changing their value.

Rounding can be done to a certain number of decimal places or to a certain number of significant figures. For example, the number 3.14159 rounded to two decimal places would be 3.14. If we round it to three significant figures, it would be 3.14 as well.

In scientific and mathematical calculations, we often use significant figures as they help to show the precision of the original measurement.

Understanding measures and accuracy is key to interpreting and using numbers in real-world contexts. By understanding these concepts, you can make meaningful comparisons, produce reliable results, and draw valid conclusions. So, the next time you’re baking and the recipe calls for exactly 200 grams of flour, you’ll know exactly what to do!

Ratio and Proportion

Ratio and proportion are two related concepts that are used to compare quantities. They are particularly useful in various everyday situations, such as cooking, shopping, and scaling things up or down.

Ratios

Let’s start with the concept of ratio. A ratio is a way of comparing quantities of the same kind. It tells us how much of one quantity there is compared to another quantity.

For instance, suppose you’re making a juice drink that requires 2 parts of orange juice to 3 parts of apple juice. The ratio of orange juice to apple juice is 2:3. This means that for every 2 cups of orange juice, you need to add 3 cups of apple juice.

Ratios can also be used to split quantities. If you and two friends find £30 and decide to split it in the ratio of 1:1:2, this means for every £1 the first person gets, the second person also gets £1, and the third person gets £2. So, the money would be split as £7.50, £7.50, and £15.

Proportions

Now let’s talk about proportion. A proportion is an equation that shows two ratios are equivalent. For example, if we have the ratio 2:3, we could write a proportion to show that this is equivalent to the ratio 4:6. We could write this as 2/3 = 4/6. This is saying that the ratio of 2 to 3 is the same as the ratio of 4 to 6.

Proportions are particularly useful when we want to scale quantities up or down. For example, if a recipe is designed to serve 4 people, but you want to prepare it for 6 people, you can use proportions to adjust the quantities of each ingredient.

Details

The Rule of Three

A helpful method to solve proportion problems is the Rule of Three (also known as cross-multiplication). Suppose you know that 4 books cost £24, and you want to find out how much 7 books would cost. You could set up a proportion:

4/24 = 7/x

Then, you cross-multiply (4 times x equals 24 times 7) and solve for x:

4x = 168

x = 42

So, 7 books would cost £42.

Mastering ratios and proportions can be a great help in your everyday life and in more advanced maths and science concepts. It’s like having a magic tool that allows you to compare, scale, and convert quantities with ease!

Algebraic Representation

Algebra is like a secret language in mathematics. Instead of using just numbers, we start to incorporate letters and symbols to represent numbers. This is the heart of algebraic representation.

Variables and Constants

In algebra, we often deal with quantities that can change. These quantities are represented by letters, such as x, y, or z, and are called variables because their values can vary. On the other hand, numbers which do not change are known as constants.

For instance, consider the equation y = 3x + 2. Here, y and x are variables, while 3 and 2 are constants.

Expressions and Equations

An algebraic expression is a mathematical phrase that can include numbers, variables, and operations (like addition, subtraction, multiplication, or division). For example, 3x – 2 is an algebraic expression.

An algebraic equation, on the other hand, is like a statement. It says that two things are equal. It consists of two algebraic expressions separated by an equal sign (=). For instance, 3x – 2 = 7 is an algebraic equation.

Solving Algebraic Equations

Solving an algebraic equation means finding the value of the variable that makes the equation true. For example, to solve the equation 3x – 2 = 7, we need to find the value of x that makes the left side (3x – 2) equal to the right side (7). By adding 2 to both sides and then dividing by 3, we find that x equals 3.

Formulas and Functions

A formula is a type of algebraic equation that shows a relationship between different variables. For instance, the formula for the area of a rectangle is A = lw, where A represents the area, l the length, and w the width. By knowing the length and width, you can find the area, or vice versa.

A function is a special type of formula that takes an input, does something to it, and gives an output. In a function like f(x) = 2x + 3, x is the input, and f(x) is the output. For any value of x that you input, the function will double it and then add three to give the output.

Algebraic representation allows us to solve more complex problems, create mathematical models of real-world situations, and explore the relationships between different quantities. So, it’s like unlocking a new level in the game of mathematics!

Place Value and Ordering

Understanding how numbers work is fundamental to the study of mathematics, and two key concepts in this understanding are place value and ordering.

Place Value

In our number system, the position of a digit in a number determines its value, and this is known as the place value of the digit.

Let’s consider a three-digit number like 345. The ‘5’ is in the ones place, the ‘4’ is in the tens place (representing 4 tens or 40), and the ‘3’ is in the hundreds place (representing 3 hundreds or 300). So, the number 345 actually represents the sum of 300, 40, and 5.

Place value continues to the right of the decimal point too. In a number like 34.56, the ‘5’ is in the tenths place (representing 5 tenths or 0.5) and the ‘6’ is in the hundredths place (representing 6 hundredths or 0.06).

Understanding place value is crucial when adding, subtracting, multiplying, and dividing numbers, as well as when rounding numbers to the nearest ten, hundred, or other place value.

Ordering

Ordering is about arranging numbers according to their value. This could be in increasing order (from smallest to largest) or decreasing order (from largest to smallest).

For example, if we have the numbers 14, 27, 9, and 35, we can order them from smallest to largest as 9, 14, 27, 35. If we wanted to order them from largest to smallest, the order would be 35, 27, 14, 9.

Ordering numbers is a fundamental skill in mathematics, as it helps us compare numbers, understand number sequences, and solve problems. It’s also useful in real-life situations, like when you want to compare prices while shopping, or when you’re checking the scores of your favourite sports teams.

In the grand scheme of mathematics, place value and ordering form the basis for understanding how numbers work, allowing us to perform calculations, make comparisons, and solve problems effectively. It’s like knowing your ABCs before you start to read and write!

Estimation

In many situations, we don’t need an exact number, but an approximate one will do. Whether you’re trying to guess the number of people in a crowd, figuring out how much time you’ll need to complete a task, or determining how much your groceries will cost before reaching the checkout counter, you’re using estimation.

Estimation is a way of getting a quick, rough idea of a quantity or a result. It’s faster than precise calculation and, while it may not be exact, it gives you a good sense of the ballpark figure.

Rounding

One of the main ways to estimate is by rounding. This involves reducing the number of digits in a number while trying to keep its value close to what it was.

For example, if a bag of apples costs £2.73, you might round this to £3 when estimating the total cost of your shopping. If you’re trying to estimate the time it takes to travel 27 kilometres at a speed of about 70 kilometres per hour, you might round 27 up to 30 because it makes the mental calculation much easier.

Estimation in Arithmetic

Estimation is also useful when doing arithmetic.

For addition and subtraction, you can round each number to the nearest ten, hundred, thousand, etc., and then add or subtract. For example, to estimate the sum of 37 + 78, you might round 37 down to 30 and 78 up to 80, making the calculation 30 + 80 = 110.
For multiplication and division, you can round one or both of the numbers to an easier number to work with. For instance, to estimate the result of 37 x 20, you might round 37 down to 30, and then calculate 30 x 20 = 600.

Benefits of Estimation

Estimation is a powerful tool that can:

Make complex calculations simpler.
Help you to quickly judge the reasonableness of an answer. For instance, if you’re calculating the cost of 15 items priced at £3 each, and you get £150, an estimate can tell you that the answer should be closer to £45, showing you that there might be an error in your calculations.
Aid in decision-making when an exact number isn’t needed.

Being good at estimation can save you time and effort, and also improve your number sense. It’s like having a mathematical intuition that can guide you in solving problems and making decisions.

Indices and Powers

Have you ever noticed small numbers written above and to the right of other numbers in math problems? Those are indices, also known as powers or exponents. They’re a way of showing that a number is multiplied by itself a certain number of times.

Understanding Indices

An expression like 2^3 (read as “two to the power of three” or “two cubed”) means that the number 2 is being multiplied by itself three times: 2 x 2 x 2, which equals 8.

In this expression, the ‘2’ is the base, and ‘3’ is the exponent or index. The base is the number that’s being multiplied, and the exponent tells you how many times the base is being multiplied by itself.

Special Exponent Rules

There are also some special rules when dealing with indices:

Any number to the power of 1 is just the number itself. For example, 7^1 = 7.
Any number (except zero) to the power of 0 is 1. So, for instance, 7^0 = 1.
Negative exponents mean you take the reciprocal of the base. For instance, 2^-3 = 1/(2^3) = 1/8.

Powers of Ten

Powers of ten are particularly important because our number system is based on ten. When you see something like 10^3, that means 1 followed by 3 zeroes, or 1000. Similarly, 10^-3 means 1 divided by 1000, or 0.001.

Square Roots and Cube Roots

Square roots and cube roots are the inverse operations of squaring (raising to the power of 2) and cubing (raising to the power of 3). The square root of a number is what you’d need to square to get that number. So, since 3 x 3 = 9, the square root of 9 is 3. Similarly, since 2 x 2 x 2 = 8, the cube root of 8 is 2.

Uses of Indices

Indices are used in many areas of mathematics and science, including algebra, geometry, physics, and engineering. They help simplify calculations and notations, especially when dealing with very large or very small numbers.

Understanding indices and powers is like having a superpower that allows you to handle repetitive multiplication with ease, work with extremely large or small numbers, and understand deeper mathematical concepts. It’s a stepping stone to more advanced mathematical topics.

Laws of Arithmetic

The laws of arithmetic, also known as the properties of arithmetic, are fundamental principles that apply to numbers and calculations. They provide the foundation for all of mathematics. Let’s explore these laws:

Commutative Laws

The commutative laws state that the order in which you add or multiply numbers does not affect the result. This means that:

For addition: a + b = b + a. For example, 3 + 5 = 5 + 3.
For multiplication: a × b = b × a. For example, 4 × 7 = 7 × 4.

However, please note that these laws do not apply to subtraction and division.

Associative Laws

The associative laws state that the way you group numbers when adding or multiplying does not change the result. This means that:

For addition: (a + b) + c = a + (b + c). For example, (2 + 3) + 4 = 2 + (3 + 4).
For multiplication: (a × b) × c = a × (b × c). For example, (3 × 4) × 5 = 3 × (4 × 5).

Again, these laws do not apply to subtraction and division.

Distributive Law

The distributive law combines addition and multiplication. It states that multiplying a number by a group of numbers added together is the same as doing each multiplication separately. In other words, a × (b + c) = a × b + a × c. For example, 4 × (5 + 6) = 4 × 5 + 4 × 6.

Identity Laws

The identity laws state that there are certain numbers, known as identity elements, that do not change other numbers when added or multiplied:

The identity element for addition is 0. This is because adding zero to any number does not change the number, i.e., a + 0 = a. For example, 5 + 0 = 5.
The identity element for multiplication is 1. This is because multiplying any number by one does not change the number, i.e., a × 1 = a. For example, 7 × 1 = 7.

Inverse Laws

The inverse laws state that every number has an inverse that can reverse the effect of addition or multiplication:

The additive inverse of a number a is -a, because a + (-a) = 0. For example, the additive inverse of 5 is -5 because 5 + (-5) = 0.
The multiplicative inverse of a number a is 1/a (except for zero, which does not have a multiplicative inverse), because a × 1/a = 1. For example, the multiplicative inverse of 4 is 1/4 because 4 × 1/4 = 1.

Understanding and applying these laws of arithmetic is like having a solid toolset for mathematics. They simplify calculations, help you solve problems more efficiently, and form the foundation for algebra and more advanced math concepts.

Laws of Exponents

Exponents, or indices, are a powerful mathematical tool, and they have their own set of laws that help simplify calculations involving powers. These laws make it easier to perform operations on numbers raised to powers, and they’re crucial in many areas of mathematics and science. Let’s delve into these laws:

Product of Powers Law

The product of powers law states that when you multiply two powers with the same base, you keep the base and add the exponents.

In mathematical terms, a^m × a^n = a^(m+n). For example, 2^3 × 2^4 = 2^(3+4) = 2^7.

Quotient of Powers Law

The quotient of powers law states that when you divide two powers with the same base, you keep the base and subtract the exponents.

Mathematically, a^m ÷ a^n = a^(m-n). For example, 5^7 ÷ 5^2 = 5^(7-2) = 5^5.

Power of a Power Law

The power of a power law states that when you raise a power to another power, you keep the base and multiply the exponents.

In mathematical notation, (a^m)^n = a^(mn). For example, (3^2)^4 = 3^(2×4) = 3^8.

Zero Exponent Law

The zero exponent law states that any non-zero number raised to the power of zero is 1.

Mathematically, a^0 = 1. For example, 10^0 = 1.

Please note that 0^0 is an indeterminate form, meaning it is not clearly defined.

Negative Exponent Law

The negative exponent law states that a number with a negative exponent can be rewritten as the reciprocal of the number with a positive exponent.

In mathematical notation, a^-m = 1/a^m. For example, 5^-3 = 1/5^3.

Power of a Product Law

The power of a product law states that a product raised to an exponent is equal to each part of the product raised to that exponent.

Mathematically, (ab)^m = a^m × b^m. For example, (2×3)^4 = 2^4 × 3^4.

Power of a Quotient Law

The power of a quotient law states that a quotient raised to an exponent is equal to the numerator raised to the exponent divided by the denominator raised to the exponent.

In mathematical terms, (a/b)^m = a^m / b^m. For example, (4/2)^3 = 4^3 / 2^3.

Knowing these laws of exponents is like knowing the rules of the road for mathematics. They guide you in the right direction and make your mathematical journey smoother and more efficient, whether you’re solving problems or exploring new concepts.

Laws Related to Fractions

Fractions represent a part of a whole and play an important role in mathematics. Just like other numbers, fractions follow specific rules or laws when you perform mathematical operations on them. Let’s explore these laws:

Law of Equivalent Fractions

Equivalent fractions are different fractions that represent the same quantity. You can create equivalent fractions by multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number.

For instance, the fractions 1/2, 2/4, 3/6, and 4/8 are all equivalent because they represent the same quantity.

Addition and Subtraction Laws

Adding or subtracting fractions requires a common denominator, which is a common multiple of the denominators of the fractions.

When adding or subtracting fractions with the same denominator, you simply add or subtract the numerators and keep the denominator the same. For example, 3/7 + 2/7 = 5/7 and 5/7 – 2/7 = 3/7.
When adding or subtracting fractions with different denominators, you must first find a common denominator, change each fraction to an equivalent fraction with the common denominator, and then add or subtract the numerators. For instance, to add 1/4 and 2/3, you might use 12 as a common denominator, changing the fractions to 3/12 and 8/12, so 1/4 + 2/3 = 3/12 + 8/12 = 11/12.

Multiplication Law

Multiplying fractions is straightforward: you simply multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator. For example, 2/3 × 4/5 = 8/15.

Division Law

Dividing fractions involves flipping (finding the reciprocal of) the second fraction and then multiplying. This process is often described as “invert and multiply”. For example, to divide 3/4 by 2/5, you would invert the 2/5 to get 5/2, and then multiply: 3/4 ÷ 2/5 = 3/4 × 5/2 = 15/8.

Simplification Law

A fraction is in simplest form when the numerator and the denominator are only divisible by 1 (they’re coprime). You can simplify a fraction by dividing both the numerator and the denominator by their greatest common divisor. For example, the fraction 8/12 can be simplified to 2/3 by dividing both 8 and 12 by 4.

These laws related to fractions are like a recipe for handling fractions correctly. They provide you with step-by-step procedures for adding, subtracting, multiplying, and dividing fractions, as well as creating equivalent fractions and simplifying fractions. Understanding and applying these laws is crucial in mathematics and can be helpful in everyday life as well.

Laws Related to Percentages

Percentages are a way of expressing a fraction or a part of a whole out of 100. They’re used extensively in daily life, from calculating discounts and interest rates to understanding statistics. Understanding the rules or laws of percentages can make these calculations much easier.

Conversion Laws

Percentages, fractions, and decimals are different ways of representing the same thing, and they can be converted back and forth:

To convert a percentage to a decimal, divide the percentage by 100. For example, 25% = 25/100 = 0.25.
To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.75 = 75%.
To convert a fraction to a percentage, divide the numerator by the denominator and multiply by 100. For example, 3/4 = 3 ÷ 4 × 100 = 75%.
To convert a percentage to a fraction, write the percentage as a fraction out of 100 and simplify if possible. For example, 20% = 20/100 = 1/5.

Percentage of a Quantity

To find a percentage of a quantity, convert the percentage to a decimal and multiply by the quantity. For example, to find 20% of 50, you would calculate 0.20 × 50 = 10.

Percentage Increase and Decrease

To increase a quantity by a certain percentage, find the percentage of the quantity and add it to the original quantity. For example, to increase 80 by 15%, calculate 15% of 80 (which is 12) and add it to 80, giving 92.
To decrease a quantity by a certain percentage, find the percentage of the quantity and subtract it from the original quantity. For example, to decrease 80 by 15%, calculate 15% of 80 (which is 12) and subtract it from 80, giving 68.

Percentages Greater Than 100%

Percentages can be greater than 100%. A percentage greater than 100% refers to a proportion that’s greater than the whole. For example, 200% of a quantity is twice the quantity.

Percentage Change

Percentage change, including percentage increase and decrease, is calculated by finding the absolute change between the old and new quantity, dividing by the original quantity, and then multiplying by 100.

For instance, if a price rises from $50 to $60, the percentage increase is calculated as (($60 – $50)/$50) × 100 = 20%.

Understanding these laws related to percentages can help make sense of various real-world situations, from calculating discounts and taxes to interpreting data and statistics. It’s a useful skill in both academic and everyday contexts.

Laws Related to Ratios and Proportions

Ratios and proportions are fundamental concepts in mathematics that express the relationship between quantities. They have their own laws or properties that guide us in solving problems or making comparisons. Let’s explore these laws:

Equality of Ratios

Two ratios are equal if the product of the means equals the product of the extremes. This is called the cross-multiplication property of proportions. In the proportion a/b = c/d, a and d are the extremes, and b and c are the means. This property states that ad = bc.

For example, in the proportion 3/4 = 6/8, the product of the extremes (3 and 8) equals the product of the means (4 and 6), confirming that the two ratios are equal.

Proportional Division Law

If a, b, c, and d are in proportion (i.e., a/b = c/d), then their differences are also in proportion. That is, (a – b) / b = (c – d) / d. For example, if 2/4 = 3/6, then (2 – 4) / 4 = (3 – 6) / 6, i.e., -2 / 4 = -3 / 6.

Ratios and Fraction Equivalence

A ratio can be considered as a fraction. When a ratio a:b is written in fractional form, it is a/b. Therefore, all laws pertaining to fractions can be applied to ratios as well.

For example, the ratio 2:4 can be simplified in the same way as the fraction 2/4, giving a simplified ratio of 1:2.

Inverse Ratio Law

If we have a ratio a:b, then the inverse ratio is b:a. For example, if the ratio of boys to girls in a class is 3:2, the ratio of girls to boys is the inverse, i.e., 2:3.

Compound Ratio Law

Compound ratios are the result of combining two or more ratios. The compound ratio of the ratios a:b and c:d is (ac) : (bd).

For example, the compound ratio of 2:3 and 4:5 is (24) : (35), i.e., 8:15.

Understanding these laws related to ratios and proportions will help in solving mathematical problems efficiently and in making sense of different real-world scenarios, from cooking recipes to planning a trip.

Test Yourself – GCSE Maths – Numbers

Write the following fraction in simplest form: 18/24

The fraction 18/24 in simplest form is 3/4

Convert 0.45 into a percentage

0.45 converted into a percentage is 45%

John wants to increase the number of hours he spends studying from 15 hours a week to 20 hours a week. What is the percentage increase?

The percentage increase is ((20-15)/15)*100 = 33.33%

Calculate the value of 5^3 × 5^2 using the laws of exponents

5^3 × 5^2 = 5^(3+2) = 5^5 = 3125

What is the value of 2^-3 based on the law of negative exponents?

2^-3 = 1/2^3 = 1/8

Are the ratios 4:6 and 14:21 proportional? Justify your answer

Yes, the ratios are proportional because 4/6 = 14/21. Both simplify to the ratio 2/3

If the ratio of apples to oranges in a basket is 3:2, what is the inverse ratio?

The inverse ratio of 3:2 is 2:3

Given the proportion 9/12 = 15/20, confirm the equality of this proportion using the property of proportions.

Using the property of proportions, 9 * 20 = 12 * 15. Both sides equal 180, thus confirming the equality.

Make an estimation: 499 + 259 + 3,791

A good estimation would be 500 + 260 + 3800 = 4560

Write 37.085 in words, according to place value and ordering

37.085 is read as “thirty-seven point zero eight five”

The value of a car depreciates by 20% each year. If the car is currently worth £15,000, what will it be worth after 3 years?

After 1 year, the car will be worth £15,000 * 0.80 = £12,000. After 2 years, it will be worth £12,000 * 0.80 = £9,600. After 3 years, it will be worth £9,600 * 0.80 = £7,680.

Solve for x: 2^(3x – 2) = 16.

We can rewrite 16 as 2^4, therefore the equation becomes 2^(3x – 2) = 2^4. Hence, 3x – 2 = 4. Solving for x gives x = 2.

The ratio of boys to girls in a class is 2:3. If there are 4 more girls than boys, how many students are there in total?

If the ratio is 2:3 boys to girls, and there are 4 more girls than boys, then there are 8 boys and 12 girls in the class, giving a total of 20 students.

Using the formula for compound interest, A = P(1 + r/n)^(nt), calculate how much a £500 investment would be worth after 3 years with an annual interest rate of 4% compounded quarterly.

Using the formula with P=£500, r=4/100=0.04, n=4, and t=3, A = £500(1 + 0.04/4)^(4*3) = £562.43 approximately.

Convert 1.75 to a fraction and simplify it.

1.75 as a fraction is 1 3/4 or 7/4 when written as an improper fraction.

Calculate the value of the following expression using the correct order of operations (BIDMAS/BODMAS): 3^2 * (2+2) ÷ 4 + 10^0.

Following the order of operations, the value of the expression is 3^2 * 4 ÷ 4 + 1 = 9 + 1 = 10.

If the ratio of the sides of two squares is 3:4, what is the ratio of their areas?

The ratio of the areas of two squares is the square of the ratio of their sides. So, if the ratio of their sides is 3:4, the ratio of their areas is 3^2 : 4^2 = 9:16.