Even though math is considered one of the hardest GCSE Subjects. It is a subject that many students find intimidating, mastering its complexities can open up numerous pathways in academia and future careers. Moreover, certain topics in GCSE Maths are notoriously perceived as more challenging than others, often leading to increased anxiety among students. Consequently, this article aims to shed light on these challenging topics, provide step-by-step solutions to some of the hardest GCSE maths questions, and offer practical advice to help students tackle their weaknesses and boost their confidence before the exam. Ultimately, this Maths exam is unquestionably one of the most important assessments in a student’s educational journey in the United Kingdom.

The Importance of Mastering the GCSE Maths

To achieve top grades in GCSE Maths, students need to master hard maths topics such as: Trigonometry, advanced algebraic manipulation and simultaneous equations. They are essential subjects that often form the foundation for more difficult problems. Getting a solid grip on these topics can dramatically impact your exam performance and set you up for success in future studies. For students who excel at GCSE level and want to progress further, A Level Further Maths builds on these concepts with even more challenging material – understanding the connections between these qualification levels can really help with long-term planning.

GCSE maths topics

While preparing for this exam, you should know that certain subjects on the syllabus are known to be more difficult, frequently presenting obstacles that can reduce your chances of receiving excellent scores. It’s important to realise why some parts of the gcse maths topics are challenging.

To achieve the best grades, students must overcome these hard Maths Questions, which are sometimes caused by difficult concepts, abstract thought, or a lack of background information. Moreover, students who successfully navigate these difficult areas develop confidence and improve their problem-solving skills, ultimately becoming skilled mathematicians. In addition, the GCSE Maths curriculum’s most challenging topics will be thoroughly covered in the sections that follow, along with step-by-step solutions to challenging problems and study techniques that will result in notable progress.

Simultaneous Equations

Simultaneous equations represent a key area of focus in GCSE maths, often involving both quadratic and linear equations. Students are expected to either graphically solve these systems or employ algebraic methods such as substitution or elimination. A further challenge arises when these equations are non-linear, pushing even the brightest students to their limits.

Formulas: For linear equations, we frequently employ:

$ax+by=c$ $dx+ey=f$

To solve simultaneous equations:

1. Rearrange equations if necessary.
2. Use substitution or elimination methods to find values for x and y.

Example: Solve the following equations:

• 2x + 3y = 6
• x – y = 2

Solution: Using the elimination method, From equation (2), x = y + 2.

Substituting into equation (1):

2(y + 2) + 3y = 6

2y + 4 + 3y = 6

5y + 4 = 6

5y = 2

y = 2/5

Substituting back to find x:
x = (2/5) + 2 = (12/5)
Final results: x = 12/5, y = 2/5.

Advanced Algebraic Manipulation

This topic encompasses crucial skills like factorising polynomials and completing the square. Each element of algebraic manipulation can become complex, especially when students are pushed to simplify difficult expressions or solve higher-level equations. Deep familiarity with these concepts is vital for solving increasingly difficult problems.

Example of Factorising: Factorise the quadratic expression x² – 5x + 6.

Solution: to factor it, find two numbers that multiply to 6 (the constant term) and add to -5 (the coefficient of x). The numbers -2 and -3 meet these criteria.
Thus, the factorisation is: (x – 2)(x – 3).

Probability and Statistics

The world of probability is both fascinating and challenging. Topics like probability trees and complex probability scenarios can confuse students, particularly when dealing with conditional probabilities. Understanding and navigating these concepts are essential for applying statistical principles and interpreting various data sets in practical situations.

Diagram: Probability Tree: Event A – 2 outcomes
/ \
P   1-P
Complex Probability Example:

A bag contains 3 red, 2 blue, and 5 green balls. What is the probability of drawing 2 red balls without replacement?

Solution:
The probability of drawing the first red ball:

P(Red 1) = 3/10
After removal, the remaining balls are 9.

P(Red 2) = 2/9
Therefore, the total probability is: P(Red 1 and Red 2) = (3/10) * (2/9) = 6/90 = 1/15.

Trigonometry and Geometry

Trigonometry, especially regarding the higher-level Pythagoras theorem, sine/cosine rules, and circle theorems, can be one of the hardest topics in GCSE maths. These concepts require a solid understanding of relationships within geometric shapes and angles, making them difficult for students who lack visual-spatial reasoning skills. Key Concepts:

Pythagorean Theorem: a² + b² = c²

Example: Find the length of the hypotenuse if one side is 3 units and the other side is 4 units.

Solution: Using the Pythagorean theorem:
c² = 3² + 4²
c² = 9 + 16
c² = 25
c = 5 units.

The Sine Rule

The Sine Rule relates the sides of a triangle to the sines of their opposite angles. It is written as:

$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$$

This formula is used to calculate missing sides or angles in a triangle when enough information is provided.

Sine Rule Example

Given a triangle ABC:

• Side $a$ = 7 cm (opposite angle A).
• Angle $A$ = 40°.
• Angle $B$ = 65°.

Find the length of side $b$.

Solution:

Step 1: Apply the Sine Rule

$$\frac{a}{\sin A}=\frac{b}{\sin B}$$

Substitute the known values:

$$\frac{7}{\sin 40°}=\frac{b}{\sin 65°}$$

Step 2: Rearrange to Find $b$

$$b=\frac{7\sin 65°}{\sin 40°}$$

Step 3: Calculate the Values

$$b=\frac{70.9063}{0.6428}=9.87cm$$

Final Answer: The length of side $b$ is approximately 9.87 cm.

Calculus (If applicable)

While calculus may not dominate the GCSE Maths syllabus, it nonetheless plays a crucial role in shaping students’ understanding of higher mathematics concepts. This section will provide students with an introductory overview of differentiation and integration as relevant to the GCSE Maths exam, along with practical examples to illustrate these concepts.

Understanding Differentiation

Differentiation is the process of finding the derivative of a function, which represents the rate at which one quantity changes with respect to another. In the context of GCSE Maths, differentiation helps ascertain slopes of curves, optimise functions, and solve problems related to motion and areas under curves.

Key Concept: The Derivative

Basic Differentiation Rules

The derivative of a function $f\left(x\right)$ is denoted as $f^{‘}\left(x\right)$ or $\frac{d}{y}dx$.

Basic Differentiation Rules:

1. The Power Rule:

If $f\left(x\right)=a{x}^n$, then $f^{‘}\left(x\right)=na{x}^{n–1}$.

2. The Constant Rule:

The derivative of a constant is zero:

$\frac{d}{c}dx=0$.

3. The Sum Rule:

The derivative of a sum is the sum of the derivatives:

$\frac{d}{u+v}dx=\frac{\mathrm{du}}{\mathrm{dx}}+\frac{\mathrm{dv}}{\mathrm{dx}}$.

Example of Differentiation:

Differentiation Problem

Problem: Differentiate $f\left(x\right)=3x^2+2x+5$.

Solution: Using the power rule:

• For $3x^2$, the derivative is $6x.$
• For $2x$, the derivative is $2.$
• The derivative of the constant $5$ is $0.$

Thus, $f^{‘}\left(x\right)=6x+2.$

Understanding Integration

Integration, on the other hand, is the reverse process of differentiation. It involves finding the integral of a function, which represents the area under the curve of that function on a given interval. It also plays a pivotal role in computing quantities like displacement, total distance traveled, and accumulated quantities over time.

Key Concept: The Indefinite Integral

Basic Integration Rules

The indefinite integral of a function $f\left(x\right)$ is denoted as $\int f\left(x\right),dx$ and includes an arbitrary constant $C$ because the derivative of a constant is zero.

Basic Integration Rules:

1. Power Rule for Integration:

If $f\left(x\right)=a{x}^n$, then:

$$\int f\left(x\right),dx=\frac{a}{n+1}{x}^{n+1}+C,\text{(for}n\ne –1\text{)}.$$

2. Integral of a Constant:

The integral of a constant $a$ is:

$$\int a,dx=ax+C.$$

Example of Integration

Integration Example

Problem: Integrate the function $g\left(x\right)=6x+4$.

Solution:

Using the power rule of integration:

For $6x$:

$$\int 6x,dx=\frac{6}{1+1}{x}^{1+1}=3x^2.$$

For $4$:

$$\int 4,dx=4x.$$

Combining these gives:

$$\int g\left(x\right),dx=3x^2+4x+C.$$

Application of Differentiation and Integration in GCSE Problems

Understanding both differentiation and integration can aid in tackling problems that may be challenging at first glance.

Example Application of Differentiation: Students may be asked to determine the maximum height of a projectile described by a quadratic function. Students can find critical points that indicate maximum or minimum values by deriving the function and setting the derivative equal to zero.

Example Application of Integration: Questions might ask for the area under a curve described by a function between two points (e.g., the x-axis from ( x = a ) to ( x = b )). Students would apply definite integral principles to compute the area.

Practice Regularly: Solve a variety of problems involving differentiation and integration to familiarise yourself with different functions and scenarios.

Hard Maths Questions from GCSE Maths Exam with Solutions

Here are a few past and one of the GCSE Maths questions along with step-by-step solutions:

Question 1: Solve the following system of simultaneous equations:

3x + 4y = 10
x^2 – 2y^2 = 5

Solution:

Solve the first equation for x:

$x=\frac{10–4y}{3}$

Substitute this expression for x in the second equation:

${\frac{10–4y}{3}}^2–2y²=5$

Expand and simplify the equation:

$\frac{100–80y+16y²}{9}–2y²=5$ $100–80y+16y²–18y²=45$ $–2y²–80y+55=0$

Solve the quadratic equation for y:

Quadratic Equation Solution

Equation:

$$y=\frac{–b\pm \sqrt{b^2–4ac}}{2a}$$

Substituting values:

Given $a=–2,b=–80,c=55$, substituting into the formula:

$$y=\frac{80\pm \sqrt{6400+440}}{–4}$$

Simplifying further:

$$y=\frac{80\pm \sqrt{6840}}{–4}$$

Approximating the square root:

$$y=\frac{80\pm 82.68}{–4}$$

Final results:

$$y\approx 2.25ory\approx –12.25$$

Substitute the values of y back into the first equation to find the corresponding values of x:

Calculations for x

For $y\approx 2.25$:

$$x=\frac{10–4\left(2.25\right)}{3}\approx 1.5$$

For $y\approx –12.25$:

$$x=\frac{10–4(–12.25)}{3}\approx 19$$

Therefore, the solutions to the system of equations are approximately (1.5, 2.25) and (19, -12.25).

Question 2. Solve the equation:

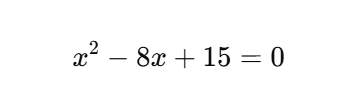
Solution:

1. Factor the quadratic equation: Look for two numbers that multiply to +15 and add to -8; these are -5 and -3.
2. Rewrite the equation: ( (x – 5)(x – 3) = 0 )
3. Set each factor to zero:
   ( x – 5 = 0 ) → ( x = 5 )
   ( x – 3 = 0 ) → ( x = 3 )
4. Answer: ( x = 5 ) or ( x = 3 )

Question 3: Algebraic Expressions

Simplify: ( 4(x + 3) – 3(2x – 4) )

Solution:

1. Distribute the terms:
   1. ( 4x + 12 – 6x + 12 )
2. Combine like terms:
   1. ( (4x – 6x) + (12 + 12) = -2x + 24 )
3. Answer: ( -2x + 24 )

Question 4: Geometry – Circles

Calculate the area of a circle with a radius of 7cm.

Calculating the Area of a Circle

Step 1: Use the formula for the area of a circle:

$$A=\pi r^2$$

Step 2: Substitute the radius:

$$A=\pi \left(72^{}\right)=\pi \left(49\right)$$

Step 3: Calculate the area:

$$A\approx 3.1449\approx 153.86 \mathrm{cm}{2}^{}$$

Answer:

$$A\approx 153.86 \mathrm{cm}{2}^{}$$

Question: 5 Differentiate the following function:

Differentiation of a Polynomial

Function:

$$f\left(x\right)=3x^4–2x^3+5x^2–7x+1$$

Solution: Use the power rule for differentiation:

$$f^{‘}\left(x\right)=12x^3–6x^2+10x–7$$

Question: 6 Solve the following inequality: 2x – 3 > 5x + 1

Solution:

1. Subtract 2x from both sides:
   1. -3 > 3x + 1
2. Subtract 1 from both sides:
   1. -4 > 3x
3. Divide both sides by 3 (remember to reverse the inequality sign when dividing by a negative number): -4/3 < x

Therefore, the solution to the inequality is: x > -4/3.

Question 7

Differentiation Example

Problem: Differentiate the following function:

$$f\left(x\right)=3x^4–2x^3+5x^2–7x+1$$

Solution: Use the power rule for differentiation:

$$f^{‘}\left(x\right)=12x^3–6x^2+10x–7$$

Study Tips for Tackling The Hardest GCSE Maths Questions

For those who are preparing for GCSE Maths exams, we have created this list to make your study process easier

• Break Down Topics: Identify hard maths questions which are challenging for you and focus on them. Create a study schedule that allocates time to these specific areas.
• Practice Past Papers: Regularly solve past exam papers under timed conditions. This helps with familiarisation of the question formats and improves speed. Students advancing to A Level should also begin exploring A Level further maths past papers to understand how GCSE concepts expand at higher levels.
• Use Online Resources: Websites such as Save My Exams provide useful revision materials and practice questions. Additionally, explore video tutorials and interactive quizzes to reinforce learning.
• Engage in Discussions: Participate in forums like Reddit, where you can ask questions, share solutions, and gain insights on difficult topics from peers and educators.
• Explore an additional Strategies to Make GCSE Maths More Manageable.

Conclusion

Mastering the hardest GCSE Maths questions can significantly boost your confidence and performance in exams. Specifically, by confronting tough problems head-on, you not only fortify your understanding of complex concepts but also develop critical thinking and problem-solving skills essential for higher education and future career paths.

Furthermore, regular practice with a focus on your weaker areas, coupled with effective resources, such as GCSE Maths tutors, can turn daunting mathematical problems into manageable tasks. As a result, this preparation allows students to approach their exams with greater assurance and composure, ultimately leading to improved grades. Embrace the challenge, and you’ll find the journey through hard maths topics not only rewarding but also enjoyable.

If you’d like more support with GCSE Maths, take a look at our answers page.