Essential GCSE Maths Formulas: Complete Revision Sheet

Maths formulas are the backbone of success in GCSE examinations, serving as crucial tools for solving a wide array of mathematical problems. From algebra to geometry, understanding these formulas can significantly enhance a student’s ability to tackle exam questions with confidence. This importance transcends all major exam boards in the UK, including OCR, AQA, and Edexcel, each of which integrates these formulas into their assessment criteria. Mastery of these mathematical tools is not just a requirement but a key to excelling in GCSE Maths.

Comprehensive List of GCSE Maths Formulas

A thorough grasp of maths formulas is indispensable for GCSE students across a variety of topics. Below is a categorized list of the essential formulas needed for the GCSE exams, tailored to cater to students’ revision needs for each mathematical area.

Algebra

Quadratic Equations:

ax² + bx + c = 0

• Simultaneous Equations: Systems of equations solved for two or more variables.
• Factorising Expressions: Breaking down complex algebraic expressions into simpler parts.

Geometry

Area and Perimeter: Formulas for different shapes including triangles, rectangles, and circles.

Volume: Calculations for the volume of cubes, spheres, cylinders, and cones.

Pythagoras’ Theorem:

a² + b² = c²

for right-angled triangles.

Trigonometry

Sine Rule: ^a⁄_{sin A} = ^b⁄_{sin B} = ^c⁄_{sin C}

Cosine Rule: c² = a² + b² – 2ab cos C

Area of a Triangle: ½ab sin C

Probability

• Probability of Independent and Dependent Events: Calculations that include additions and multiplications of probabilities.
• Expected Value: The mean of a probability distribution, representing the average outcome.

Statistics

• Mean, Median, Mode: Measures of central tendency.
• Standard Deviation: A measure of the amount of variation or dispersion in a set of values.

To assist in your revision, a downloadable PDF containing all these formulas in a well-organised format is available. This resource is invaluable during revision time, allowing students to have quick and easy access to the formulas needed for their GCSE maths exams.

Detailed Explanations of Key Formulas – GCSE Maths Formula Sheet

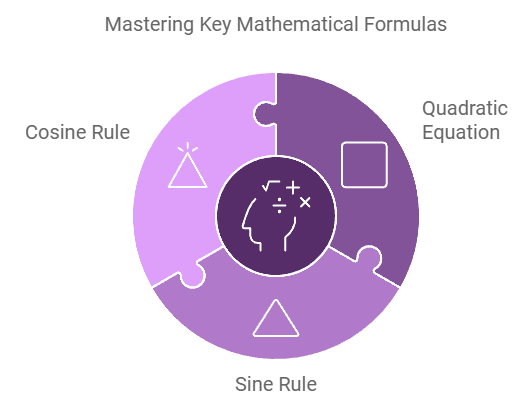
Understanding how to apply key mathematical formulas can drastically improve problem-solving skills in GCSE Maths. Below, we explore complex formulas like the Quadratic Equation and the Sine and Cosine Rules, providing step-by-step examples to demonstrate their use.

ax² + bx + c = 0

The solution is given by

$$x=\frac{–b\pm \sqrt{b^2–4ac}}{2a}$$

These trigonometric rules are crucial for solving problems in triangles that are not right-angled.

• Sine Rule: Used when we know either two angles and one side or two sides and a non-included angle

$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$$

Example: Find side a in a triangle where $b=10$, $B=60°$, and $A=45°$.

1. Apply the Sine Rule: $\frac{a}{\sin 45°}=\frac{10}{\sin 60°}$
2. Rearrange and solve for a: $a=\frac{10\sin 45°}{\sin 60°}\approx 8.16$

Cosine Rule: Used to find a side from two sides and the included angle or to find an angle from three sides. $c^2=a^2+b^2–2ab\cos C$

Example: Calculate the length of side c where $a=8$, $b=6$, and $C=50°$.

1. Substitute into the Cosine Rule: $c^2=8^2+6^2–2\times 8\times 6\times \cos 50°$
2. Calculate c: $c\approx 5.66$

These detailed breakdowns not only illustrate the procedure of applying these formulas but also clarify the mathematical reasoning behind each step, enabling students to understand and utilize these formulas effectively in their examinations.

Tips on How to Memorise Formulas

Memorising mathematical formulas is a key skill for GCSE students, facilitating faster recall during exams and reducing cognitive load during problem-solving. However, it’s crucial to balance raw memorisation with a deep understanding to apply these formulas correctly. Here are some techniques that can help:

Effective Memorisation vs. Understanding

• Understanding First: Before memorising a formula, it’s vital to understand what it represents and how it derives from mathematical principles. This ensures that the memorisation has context and can be applied flexibly in various situations.
• Practical Application: Regularly practice using the formula in different types of problems. This not only reinforces memory through repetition but also enhances understanding by showing how the formula functions in various scenarios.

Mnemonics: Create simple, catchy acronyms or phrases that help remember complex formulas.

For instance, the quadratic formula $a{x}^2+bx+c=0$ can be remembered with the mnemonic “ABC: Always Bring Calculator,” referring to the coefficients a, b, and c.

• Visual Aids: Diagrams and charts can be very effective, especially for geometric formulas. Visualising the formula and its components can help anchor the information in your memory.
• Repetitive Practice: Repetition is one of the most effective memory techniques. Regularly writing down formulas, saying them aloud, and using them in practice problems can significantly improve retention.
• Teach Others: Explaining a formula to someone else is a great way to reinforce your own understanding and memorisation. Teaching requires you to recall the formula and its applications, which deepens your memory connection.
• Flashcards: Use flashcards with the formula on one side and a sample problem or the formula’s name on the other. Regularly testing yourself with these can enhance recall speed and accuracy.
• Association Techniques: Link formulas with specific problems or real-world applications. Associating a formula with a particular context or problem type can trigger memory when encountering similar problems during an exam.

By combining these strategies, students can develop a robust ability to recall and apply mathematical formulas efficiently. This approach not only prepares them for their exams but also builds a foundational skill set for further studies in mathematics and related fields.

How Understanding Formulas Deepens Knowledge Across Sciences

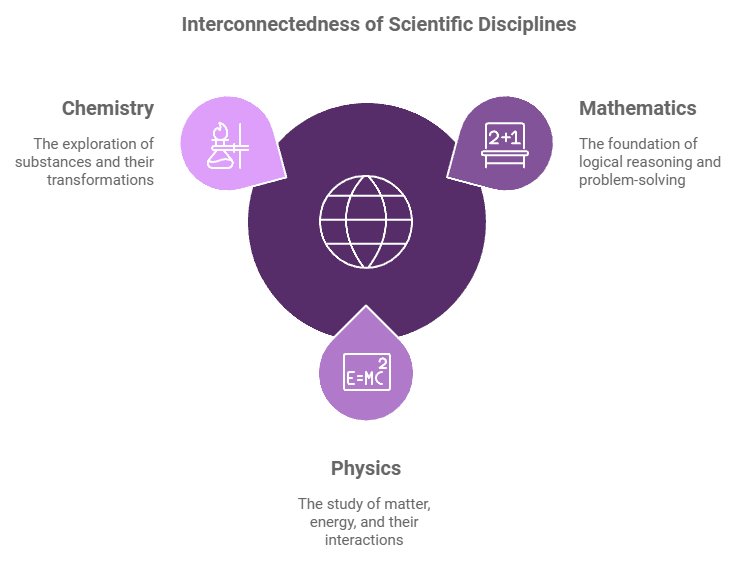
Mathematical formulas are not confined solely to the realm of mathematics; they play a significant role in other subjects such as Physics and Chemistry, demonstrating the interconnected nature of scientific disciplines. Understanding these connections can enrich students’ learning experiences and provide them with a more holistic view of how different fields interrelate.

Physics

In Physics, formulas are used to describe and calculate physical phenomena such as forces, motion, energy, and waves. For example:

• Force: Newton’s Second Law of Motion is expressed as $F=ma$ (Force equals mass times acceleration). This formula is fundamental in predicting how much an object will accelerate when a certain amount of force is applied.

• Energy: The formula for kinetic energy, $KE=\frac{1}{2}m{v}^2$ (where m is mass and v is velocity), helps in calculating the energy an object possesses due to its motion.

Chemistry

In Chemistry, formulas are crucial for determining the quantities involved in chemical reactions and solutions:

• Molar Concentration: The molar concentration of a solution can be calculated using the formula $C=\frac{n}{V}$, where C is the concentration, n is the number of moles of solute, and V is the volume of the solution in liters. This is essential for preparing solutions with precise chemical concentrations.

• Ideal Gas Law: The formula $PV=nRT$ (where P is pressure, V is volume, n is moles of gas, R is the gas constant, and T is temperature in Kelvin) is used to relate the pressure, temperature, and volume of gases.

Application Examples

• Cross-Disciplinary Problems: Students might be tasked with calculating the energy required to heat water in a kettle. Here, they could use the specific heat capacity formula from Chemistry, $q=mc\Delta T$, alongside the power formula from Physics, $P=\frac{E}{t}$, to determine both the heat energy needed and the time it would take under different power settings.

• Practical Experiments: In experiments, Physics and Chemistry often overlap, such as when measuring the electrical energy (using $E=VIt$, where V is voltage and I is current) delivered in an electrochemical cell in Chemistry.

These cross-curricular applications not only help students see the relevance of what they are learning but also enhance their problem-solving skills by applying mathematical reasoning across different contexts. This approach encourages a deeper understanding and retention of the concepts, which is beneficial for their overall academic and future career paths.

Interactive Elements

Incorporating interactive elements into the study of GCSE maths can significantly enhance engagement and understanding. Interactive quizzes and problem-solving challenges are excellent tools for reinforcing knowledge and applying mathematical formulas in various contexts.

Interactive Quizzes

• Purpose: To test the student’s ability to recall and apply formulas quickly and correctly.
• Implementation: Quizzes can be structured to include multiple-choice questions, fill-in-the-blank formulas, and even drag-and-drop elements for matching formulas with their correct applications.
• Feedback: Immediate feedback should be provided, explaining why an answer is correct or incorrect, which helps in reinforcing learning or correcting misunderstandings.

Example: An online quiz could ask students to select the correct formula for calculating the area of a circle. Once the answer is submitted, the quiz could display a brief explanation and then present a problem requiring the student to calculate the area of a circle given its radius.

Problem-Solving Challenges

• Purpose: To encourage deeper thinking and application of multiple formulas in more complex, real-world scenarios.
• Implementation: Challenges can be presented as interactive scenarios where students need to apply several concepts to progress. These could be formatted as virtual lab experiments, real-life problem simulations, or even game-based learning environments.
• Collaboration: Allowing students to work in teams on these challenges can promote discussion, enhance problem-solving skills, and encourage a collaborative learning environment.

Example: A virtual lab might simulate a situation where students must design a rollercoaster. They would need to calculate the potential and kinetic energy at different points using physics formulas, as well as the curves of the track using trigonometry.

Integration with Technology

• Educational Platforms: Tools like Kahoot!, Quizlet, or proprietary school learning management systems can be used to host these interactive quizzes and challenges.
• Customization: Teachers and educators can customize the difficulty and scope of the quizzes and challenges based on the curriculum and specific learning objectives of their students.

Integrating these interactive elements into the maths curriculum not only makes learning more engaging but also helps students to effectively internalize and apply mathematical concepts. It prepares them for GCSE exams and further educational pursuits by developing their problem-solving skills and their ability to apply knowledge in varied situations.

Common Mistakes and Misconceptions

Understanding and avoiding common mistakes in applying mathematical formulas is crucial for students to achieve success in their GCSE exams. Here we highlight some typical errors and misconceptions that can hinder a student’s ability to correctly solve problems.

Sign Errors in Trigonometry

• Problem: One of the most frequent errors in trigonometry involves incorrect signs when applying the sine, cosine, and tangent ratios, especially in different quadrants.
• Solution: Emphasize the importance of the unit circle and trigonometric identities, reinforcing the signs of trigonometric functions in each quadrant. Teaching mnemonic devices like “All Students Take Calculus” can help students remember which trigonometric functions are positive in each quadrant.

Miscalculations in Area and Volume

• Problem: Students often misapply formulas for area and volume by confusing the dimensions (length, width, height) or using the wrong units.
• Solution: Stress the importance of labelling all dimensions and converting units where necessary. Practice problems should include a variety of shapes and composite figures to ensure students are comfortable with applying the correct formulas in different contexts.

Misuse of the Quadratic Formula

• Problem: Misreading coefficients or incorrectly identifying the values of a, b, and c in the quadratic equation can lead to errors in using the quadratic formula.

• Solution: Teach students to always write down the standard form of the quadratic equation $a{x}^2+bx+c=0$ before substituting values into the quadratic formula. This practice helps prevent misidentification of coefficients.

Confusion Between Perimeter and Area Calculations

• Problem: Students often confuse the formulas for perimeter and area, particularly in polygons.
• Solution: Use visual aids to reinforce the difference between linear measures (perimeter) and square measures (area). Practice exercises should clearly distinguish between finding lengths and calculating areas.

Misinterpretation of Formula Variables

• Problem: A common error is the misinterpretation of what variables represent in a formula, leading to incorrect substitutions and results.
• Solution: Encourage students to take time to understand what each variable represents in the context of a problem. Using dimensional analysis can also help students check that their substitutions make sense dimensionally.

Incorrect Algebraic Manipulations

• Problem: Errors in algebraic manipulations such as expanding brackets or simplifying expressions can lead to incorrect applications of formulas.
• Solution: Regular practice with algebraic expressions and clear step-by-step demonstrations can help. Encouraging students to double-check their work by plugging answers back into the original equation can also catch errors before they finalize their solutions.

By addressing these common mistakes and ensuring students understand not just the “how” but also the “why” behind the formulas they use, educators can greatly enhance their students’ proficiency and confidence in mathematics. This approach not only prepares them for exams but also builds a solid foundation for future mathematical learning.

Additional Resources

Enhancing GCSE maths preparation involves not just understanding and applying mathematical formulas but also accessing various supplementary resources that can aid in deeper learning and practice. Here are some valuable resources, further readings, and tools that students can use to reinforce their maths skills:

Online Resources and Further Reading

• Khan Academy: Offers comprehensive lessons on all areas of GCSE maths with practice exercises and instructional videos.
• BBC Bitesize: Provides detailed notes and quizzes tailored to the GCSE curriculum.
• Maths Genie: A helpful resource with free GCSE and A-Level revision materials, including past papers, mark schemes, and revision notes.

Practice Sheets

• Corbettmaths: This site offers practice sheets and videos on a wide range of GCSE topics, which are great for revision and practice.
• Edexcel Online Practice: Edexcel provides practice tests and sample papers directly related to the syllabus.

Apps and Tools

• Photomath: Useful for step-by-step solutions to maths problems just by taking a picture of the equation.
• Desmos: An advanced graphing calculator ideal for visualising algebraic equations and exploring complex graphs.
• Quizlet: Great for creating custom flashcards to help memorise formulas and mathematical concepts.

Additional Learning Tools

• GeoGebra: Provides interactive geometry, algebra, statistics, and calculus applications, which are powerful tools for understanding and visualizing mathematical concepts.
• Wolfram Alpha: More than just a search engine, Wolfram Alpha computes answers for formula inputs and complex equations, providing step-by-step solutions.
• Edumentors: Connects students with expert tutors from top UK universities who offer personalised support and guidance across GCSE maths topics, ensuring targeted learning.

These resources offer various ways to engage with the material, from interactive tools and apps to comprehensive reading materials and practice exercises. They can significantly enhance the learning experience, providing students with the support they need to excel in their exams.

Conclusion

Mastering the key mathematical formulas is essential for success in GCSE exams. These formulas are not just tools for solving numerical problems; they are the building blocks for understanding complex mathematical concepts that span a variety of subjects, from geometry to physics and chemistry. As students progress in their education, the ability to quickly recall and apply these formulas becomes increasingly important, particularly under the time constraints of an exam setting.

Continual practice is vital. Regularly consulting the formula sheet and incorporating these formulas into daily study routines can transform them from abstract concepts into second nature. The use of additional resources such as interactive quizzes, practice sheets, and digital tools can further enhance understanding and retention.

Ultimately, the journey to GCSE success is marked by consistent practice and a deep understanding of mathematical principles. Students are encouraged to explore various resources and continually challenge themselves with new problems to ensure that they are fully prepared not just for their exams, but for any mathematical challenges they may face in the future.

For students seeking personalised support, Edumentors provides expert tutors from top UK universities who specialise in GCSE maths. With tailored guidance, students can focus on areas they find most challenging, enabling them to strengthen their understanding and approach exams with confidence. Find your GCSE maths tutor.