Energy Equation In Physics – Everything You Need To Know

In both GCSE and A-Level Physics, understanding energy and how it behaves is crucial. The energy equation is a fundamental concept that helps explain how energy is transferred and transformed in different systems. Whether you’re tackling questions on mechanical work or calculating power, mastering the energy equation is key to succeeding in your exams.
Additionally, this blog aims to break down the energy equation, explaining its core components and how to apply it effectively in various physics scenarios. By the end, you’ll have a solid understanding of energy principles that will not only help with exam preparation but also with real-world applications of physics. So Keep up! We’ve got you!

What is the Energy Equation?

The energy equation represents the relationship between energy, work, power, and other key variables in physics. It helps to explain how energy is transferred when forces act over distances and how power is the rate at which energy is used or transferred.

Energy Formula In Physics

Work Done (Energy) = Force × Distance

This formula is used to calculate the work done or energy transferred when a force is applied to an object over a distance. The units of force are Newtons (N), and the units of distance are meters (m), so the result will be in joules (J), which is the standard unit for energy.

• Force (F): The push or pull applied to an object.
• Distance (d): The distance over which the force is applied.

Energy = Power × Time

This equation relates energy to power and time. It’s used when you need to calculate the energy used or transferred over a given time period.

• Power (P): The rate at which work is done or energy is transferred. It is measured in watts (W).
• Time (t): The amount of time (in seconds) over which the energy is used or transferred.

By understanding these two equations, students can apply them in various physics problems, such as calculating the energy transferred in lifting an object, the power output of an engine, or the energy consumption of an electrical appliance. So, let’s talk about different types of energy equations. Keep reading!

Types of Energy Equations

Energy plays a crucial role in physics, and various equations help us calculate the different forms of energy an object can possess. Here, we’ll look at three key energy equations: kinetic energy, gravitational potential energy, and elastic potential energy.

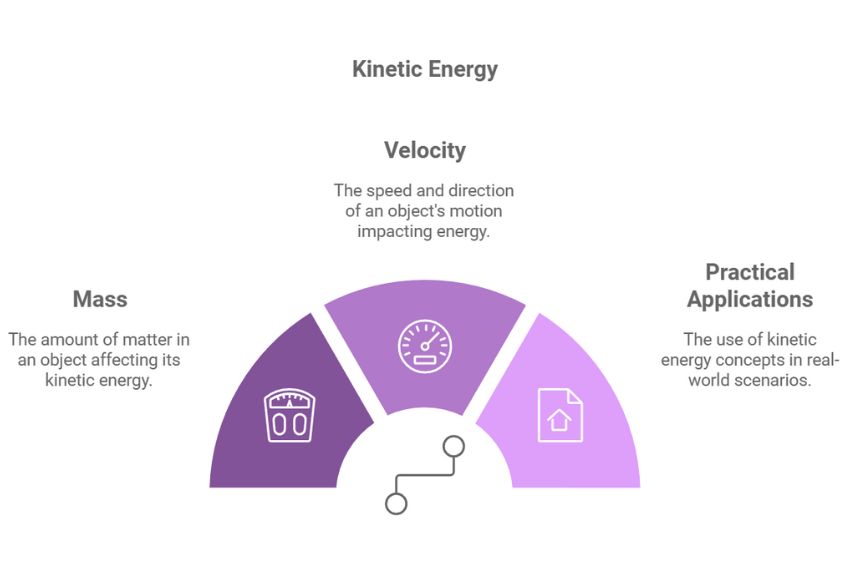
Kinetic Energy Equation:

Kinetic Energy (KE) = ½ mv²

Where:

• m is the mass of the object (in kilograms).
• v is the velocity of the object (in meters per second).

This equation represents the kinetic energy of an object, which is the energy it possesses due to its motion. The formula shows that an object with greater mass or higher velocity will have more kinetic energy.
For example, a car moving at high speed or a large object in motion will have much more kinetic energy compared to a stationary object. The equation helps us calculate the amount of energy an object has while moving. For Instance, if a 1,000 kg car is traveling at 20 m/s, the kinetic energy can be calculated as:

KE = ½ × 1000 kg × (20 m/s)² = 200,000 Joules (J)

This means the car has 200,000 Joules of kinetic energy while moving.

Gravitational Potential Energy Equation:

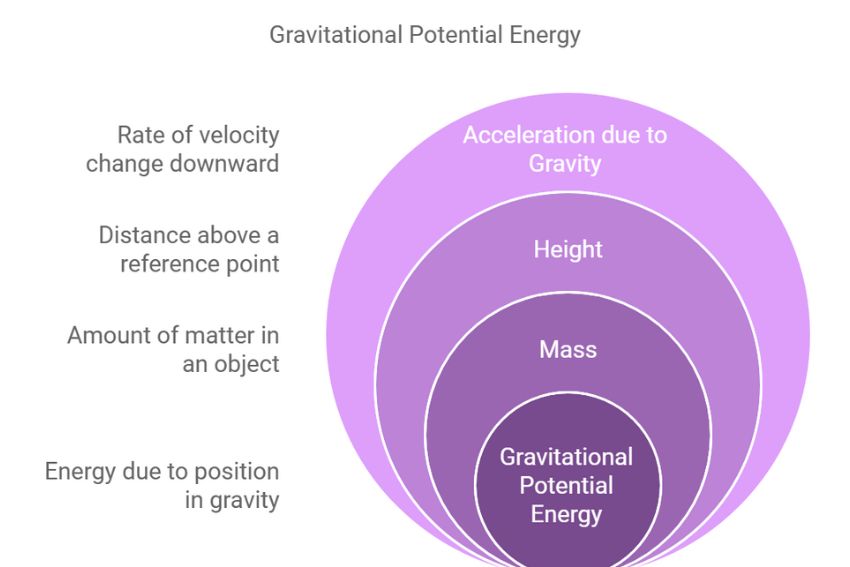
Potential Energy (PE) = mgh

Where:

• m is the mass of the object (in kilograms).
• g is the acceleration due to gravity (9.8 m/s² on Earth).
• h is the height of the object (in meters).

As you can sea this equation calculates the gravitational potential energy of an object, which is the energy it possesses due to its position relative to the Earth’s surface. The higher an object is raised, the more potential energy it gains. For example, lifting an object to a certain height in the air stores energy, which can be converted to kinetic energy when it falls.

To calculate the gravitational potential energy of a 10 kg object raised to a height of 5 meters:

PE = 10 kg × 9.8 m/s² × 5 m = 490 Joules (J)

This means the object has 490 Joules of potential energy when raised to 5 meters above the ground.

Elastic Potential Energy Equation:

Elastic Potential Energy (EPE) = ½ kx²

Where:

• k is the spring constant (in N/m), which measures how stiff the spring is.
• x is the extension or compression of the spring (in meters).

This equation calculates the elastic potential energy stored in an object when it is stretched or compressed. The more the spring is stretched or compressed (the greater the value of x), the more energy it stores. The spring constant (k) reflects the stiffness of the spring: a stiffer spring has a higher value for k.

For example, if a spring has a spring constant of 200 N/m and is stretched by 0.5 meters, the elastic potential energy stored in the spring can be calculated as:

EPE = ½ × 200 N/m × (0.5 m)² = 25 Joules (J) This means the spring stores 25 Joules of elastic potential energy when stretched by 0.5 meters.

How Energy Equations Are Used in Physics

To clarify energy equations are fundamental in Physics, as they help explain how energy is transferred, conserved, and used in various physical processes. Below, we break down key concepts such as work, energy transfer, conservation of energy, and power, and explain how energy equations are applied in real-world scenarios. So, how we use energy equation in Physics?

Work and Energy Transfer:

In physics, work is defined as the transfer of energy when a force acts on an object to move it over a distance. The formula to calculate work done (or energy transferred) is:

Work Done = Force × Distance

Where:

• Force is the push or pull applied to an object (in Newtons, N).
• Distance is how far the object is moved in the direction of the force (in meters, m).

For example, if you push a box with a force of 10 N across a distance of 5 meters, the work done (or energy transferred) would be:

Work Done = 10 N × 5 m = 50 Joules (J)

This means 50 Joules of energy has been transferred in moving the box.

Energy Conservation:

Simply put the principle of energy conservation states that energy cannot be created or destroyed, only converted from one form to another. In a closed system, the total amount of energy remains constant, even though it may change form.

For example, when you throw a ball into the air, its kinetic energy (from the motion) is converted into gravitational potential energy (as the ball rises). When the ball starts to fall, this potential energy is converted back into kinetic energy. Throughout this process, the total energy remains the same, though it changes from one form to another.

This principle is crucial for understanding the behavior of different systems and solving problems related to energy transformations, such as in mechanical systems or electrical circuits.

Power and Energy:

Power is the rate at which energy is transferred or converted. It measures how quickly energy is used or generated over time. The formula to calculate power is:

Power = Energy / Time

Where:

• Power (P) is measured in watts (W).
• Energy (E) is the total energy transferred or converted (in joules, J).
• Time (t) is the time during which energy is transferred (in seconds, s).

For example, if an electrical appliance uses 200 Joules of energy in 10 seconds, the power it uses can be calculated as:

Power = 200 J / 10 s = 20 Watts (W) This tells us the appliance consumes energy at a rate of 20 watts.

Work Done, Energy Transferred, and Power:

While work done and energy transferred refer to the amount of energy used to move an object or perform a task, power is the rate at which this energy is used or transferred.

For example:

• Work Done: Lifting a box from the floor to a shelf (energy required to overcome gravity).
• Energy Transferred: The energy used by the box to move.
• Power: The rate at which you lift the box (how fast energy is used).

In everyday scenarios, such as using electrical appliances, understanding power helps us calculate how much energy is consumed over time. For example, a 100 W light bulb uses 100 joules of energy every second. Knowing the power rating of an appliance allows you to estimate energy usage and understand electricity bills.

Real-World Applications of Energy Equations

Of course, energy equations are not just theoretical. they are applied across various real-world systems, from mechanical devices to electrical circuits and renewable energy systems. Below are some key examples of how energy equations are used in everyday life.

Mechanical Systems:

In mechanical systems, energy equations are essential for calculating and understanding how energy is transferred and used.

Kinetic Energy of a Moving Car:

The equation for kinetic energy helps us calculate the energy of an object in motion, such as a car. The formula is: Kinetic Energy (KE) = ½ mv²

Where:

• v is its velocity.
• m is the mass of the car

For example, a car with a mass of 1,000 kg moving at 20 m/s will have:
KE = ½ × 1000 kg × (20 m/s)² = 200,000 Joules (J)
This calculation shows the amount of energy the car has due to its motion.

Gravitational Potential Energy of a Lifted Object:

When lifting an object, the energy required is stored as gravitational potential energy. The equation is:

Potential Energy (PE) = mgh

Where:

• m is the mass of the object,
• g is the gravitational field strength (9.8 m/s² on Earth),
• h is the height.

For example, lifting a 10 kg object to a height of 5 meters would require:
PE = 10 kg × 9.8 m/s² × 5 m = 490 Joules (J)
This demonstrates the energy needed to raise the object against gravity.

Energy in a Spring System (Elastic Potential Energy):

In spring systems, energy is stored when the spring is stretched or compressed. The equation for elastic potential energy is:

Elastic Potential Energy (EPE) = ½ kx²

Where:

• k is the spring constant,
• x is the extension of the spring.

For example, if a spring with a spring constant of 200 N/m is stretched by 0.5 meters, the energy stored in the spring is:

EPE = ½ × 200 N/m × (0.5 m)² = 25 Joules (J)

This shows how energy is stored when the spring is stretched.

Electrical Energy:

Energy equations also apply to electrical systems, where they help calculate energy consumption, power usage, and efficiency.

Energy Consumption in Circuits:

The equation for electrical power is: Power (P) = Voltage (V) × Current (I)

Where:

• P is power (in watts),
• V is voltage (in volts),
• I is current (in amperes).

For example, if a circuit has a voltage of 230V and a current of 3A, the power consumption is:

P = 230 V × 3 A = 690 watts (W)
Of course this tells us how much energy is consumed by the electrical device in the circuit.

Energy Usage:

Moreover to calculate the energy used by an electrical appliance, we can use the formula:

Energy (E) = Power × Time

For example, if a 100W light bulb is used for 5 hours, the energy consumed is:

E = 100 W × 5 hours = 500 watt-hours (Wh)
This helps us understand how much energy appliances consume and can assist in managing electricity bills.

Renewable Energy:

Energy equations are essential in understanding and optimizing renewable energy systems, such as wind turbines and solar panels.

Wind Turbines:

In wind turbines, energy is transferred from the wind to mechanical energy, which is then converted into electrical energy. The power generated by a wind turbine depends on the wind speed, the area swept by the turbine blades, and the efficiency of the system. A simplified equation for power from wind energy is:

Power = ½ × ρ × A × v³ × Cp

Where:

• ρ is the air density,
• A is the swept area of the turbine blades,
• v is the wind velocity,
• Cp is the coefficient of performance (which varies depending on the turbine’s efficiency).

This equation helps calculate the energy output of a wind turbine based on local wind conditions and turbine design. Therefore, it provides a valuable tool for optimizing performance.

Solar Panels:

Similarly, in solar panels, the energy equation is used to calculate the electrical power generated from sunlight. The basic formula is:

Power = Efficiency × Area × Solar Radiation

Where:

• Efficiency is the efficiency of the solar panel,
• Area is the surface area of the solar panel,
• Solar Radiation is the amount of sunlight received per unit area.

For example, a 10 m² solar panel with 20% efficiency might receive 1,000 W/m² of sunlight. The power output is:

Power = 0.2 × 10 m² × 1,000 W/m² = 2,000 watts (W)

So, this calculation helps to determine how much electricity can be generated by solar panels in specific conditions.

How To Solve Common Problems By Energy Equation? Examples:

In this section, we’ll explore how to use energy equations to solve real-world problems, step by step. We’ll work through examples that require you to calculate kinetic energy, gravitational potential energy, and elastic potential energy. These examples will also help you practice unit conversions and develop strategies for solving energy-related problems effectively.

Calculating the Kinetic Energy of a Moving Object

The kinetic energy (KE) equation is:

KE = ¹⁄₂mv²

Where:

• m = mass of the object (in kilograms, kg)
• v = velocity (in meters per second, m/s)

Example: A car with a mass of 800 kg is moving at 20 m/s. Calculate its kinetic energy.

Step 1: Plug the values into the equation

KE = ½ × 800kg × (20m/s)²

Step 2: Square the velocity:

KE = ½ × 800 × 400 = 160,000 Joules (J)

Answer: The car’s kinetic energy is 160,000 J.

Finding the Gravitational Potential Energy of an Object at Height

The gravitational potential energy (PE) equation is:

PE = mgh

Where:

• m = mass of the object (in kilograms, kg)
• g = gravitational field strength (9.8 m/s² on Earth)
• h = height (in meters, m)

Example: An object with a mass of 10 kg is lifted to a height of 5 meters. Calculate its gravitational potential energy.

Step 1: Plug the values into the equation:

PE = 10kg × 9.8m/s² × 5m

Step 2: Multiply the values:

PE = 10 × 9.8 × 5 = 490 Joules (J)

Answer: The object’s gravitational potential energy is 490 J.

Determining the Elastic Potential Energy in a Compressed Spring

The elastic potential energy (EPE) equation is:

EPE = ½ kx²

Where:

• k = spring constant (in Newtons per meter, N/m)
• x = extension or compression of the spring (in meters, m)

Example: A spring with a spring constant of 200 N/m is compressed by 0.2 meters. Calculate the elastic potential energy stored in the spring.

Step 1: Plug the values into the equation:

EPE = ½ × 200 N/m × (0.2 m)²

Step 2: Square the extension:

EPE = ½ × 200 × 0.04 = 4 Joules (J)

Answer: The elastic potential energy stored in the spring is 4 J.

Unit Conversions and Practical Tips

• Units: Always make sure that your units are consistent. For example, mass should be in kilograms (kg), velocity in meters per second (m/s), height in meters (m), and spring constant in Newtons per meter (N/m). Converting units is often necessary in real-life problems (e.g., converting grams to kilograms or kilometers to meters).
• Check your powers: When squaring a value (e.g., in the kinetic energy equation), ensure that you properly handle the units. For example, if the velocity is 20 km/h, convert it into m/s first before squaring it.
• Work systematically: Start with writing down the equation, substituting known values, and solving for the unknown. Double-check calculations, especially when dealing with multiple steps.
• Use approximations when needed: In some cases, rounding off values, such as gravitational field strength (which is usually approximated as 9.8 m/s² on Earth), may make calculations easier without significantly affecting the accuracy of the result.

Exam Relevance For Energy Equation Physics A-Level:

Energy equations are a key part of both GCSE and A-Level Physics exams. These equations are often tested in various forms, from straightforward calculations to more complex, real-world scenarios. You may be asked to calculate kinetic energy, gravitational potential energy, or elastic potential energy in an object or system. Additionally, understanding the power equation and how to calculate energy efficiency is also vital for exam success.

Additionally, in exams, students are typically required to:

• Use energy equations to calculate work done, energy transferred, and power in different scenarios.
• Apply energy conservation principles to solve problems.
• Analyze the efficiency of systems, particularly in the context of energy transfer and loss.

Being able to apply these equations correctly is not only crucial for achieving good marks but also for developing a deeper understanding of how energy operates in both theoretical and practical contexts. Therefore, mastering these equations and their applications will significantly improve your exam performance and overall understanding of physics.

Sum Up Energy Equation Topic

Understanding energy equations is essential for mastering key concepts in GCSE Physics and A-Level Physics. In particular, these equations help explain how energy is transferred, conserved, and used in various physical processes, from mechanical systems to electrical circuits. Moreover, by practicing the different types of energy equations – kinetic energy, gravitational potential energy, and elastic potential energy – you can solve real-life problems and gain a deeper understanding of the world around you.

To conclude, to truly excel, it’s important to grasp the nuances of these equations, avoid common mistakes, and apply them accurately in your exams. If, however, you find certain concepts challenging, don’t hesitate to seek support from online A-level physics tutors. They can offer personalized guidance, explain complex topics in a simple way, and provide additional resources and practice to ensure you’re fully prepared for your exams. With the right support and consistent practice, you’ll be well-equipped to tackle any energy-related question that comes your way.

FAQ’s About Energy Equation

What is the formula of energy?

The formula for energy depends on the type of energy. For kinetic energy, it’s E = ½mv². For potential energy, it’s E = mgh. These equations show how energy relates to mass, speed, and height.

What is the equation for elastic potential energy?

The equation for elastic potential energy is E = ½kx², where k is the spring constant and x is the extension of the spring.

What is the simple equation for energy?

The simplest equation for energy is E = Power × Time. This equation calculates the energy transferred or used over a period.

What is the energy equation for GCSE?

For GCSE, the energy equation commonly used is E = Work Done = Force × Distance. This relates to energy transferred when a force moves an object.

What is the equation for gravitational potential energy?

So, Potential Energy (PE) = mgh. m is the mass of the object (in kilograms).

g is the acceleration due to gravity (9.8 m/s² on Earth).

h is the height of the object (in meters).