8 Circle Theorems Visualised and Explained – GCSE Maths

Let’s learn 8 circle theorems – prepare for GCSE maths and A-level maths.

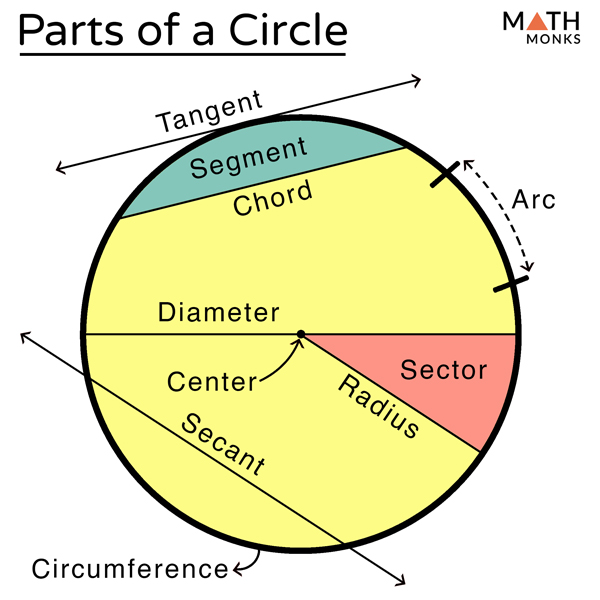
What is a Circle Theorem?

1. Angle at the Centre Theorem

This theorem states that the angle subtended at the centre of a circle by two given points on the circumference is precisely twice the angle subtended at the circumference by those same points. If A, B, and C are points on the circumference of a circle with the centre O, and ∠AOB is an angle at the centre, while ∠ACB is an angle at the circumference, then the theorem can be expressed mathematically as:

∠AOB=2×∠ACB

2. Angles in the Same Segment Theorem

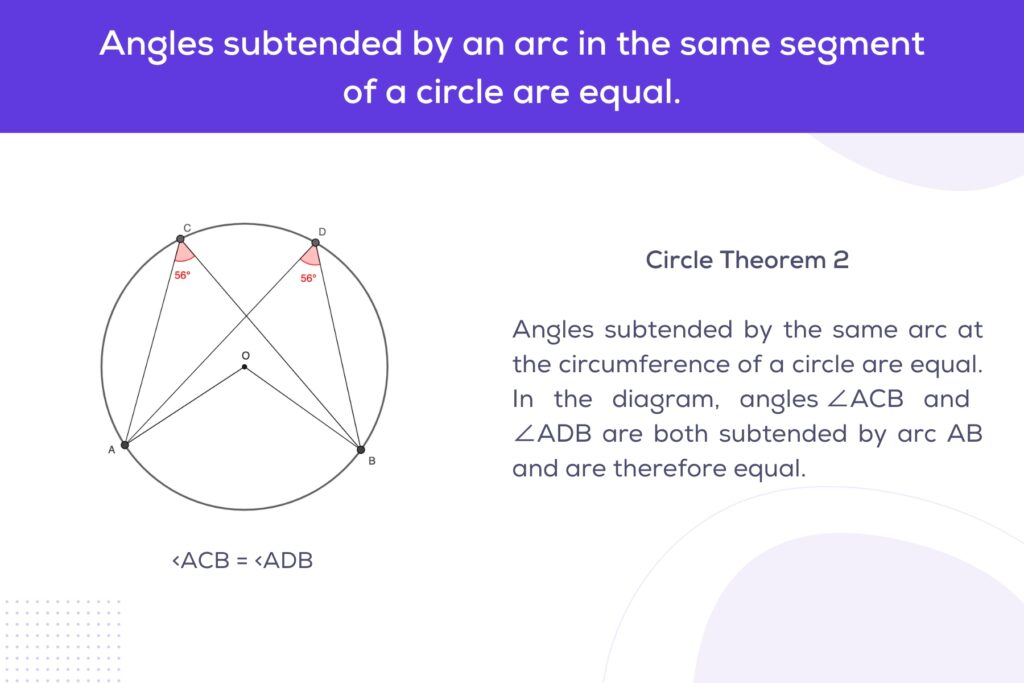
The theorem asserts that angles subtended by the same arc at the circumference of a circle are equal. In essence, if two angles are inscribed on the circumference of a circle and subtended by the same arc, they will be congruent.

∠ACB=∠ADB

3. Cyclic Quadrilateral Theorem

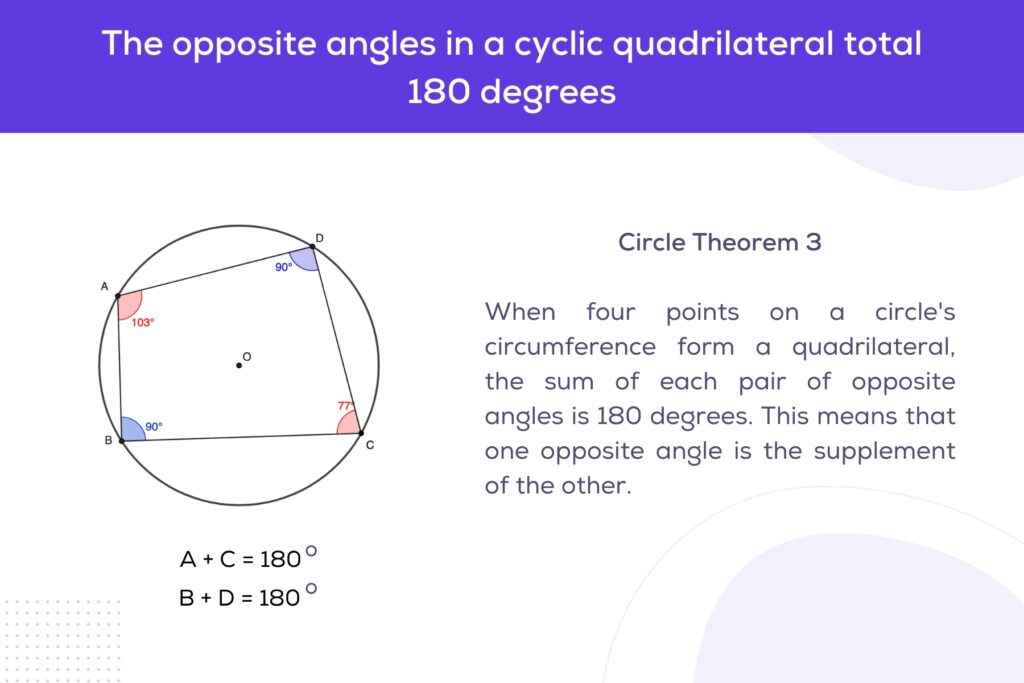
This theorem states that the sum of the opposite angles of a cyclic quadrilateral is 180 degrees. The theorem is significant because it applies to any quadrilateral where all four vertices lie on the circumference of a circle.

If we have a cyclic quadrilateral ABCD, with the vertices A, B, C, and D resting on the circumference of a circle, the theorem can be expressed as:

∠A+∠C=180∘ , ∠B+∠D=180∘

4. Angle in a Semicircle Theorem

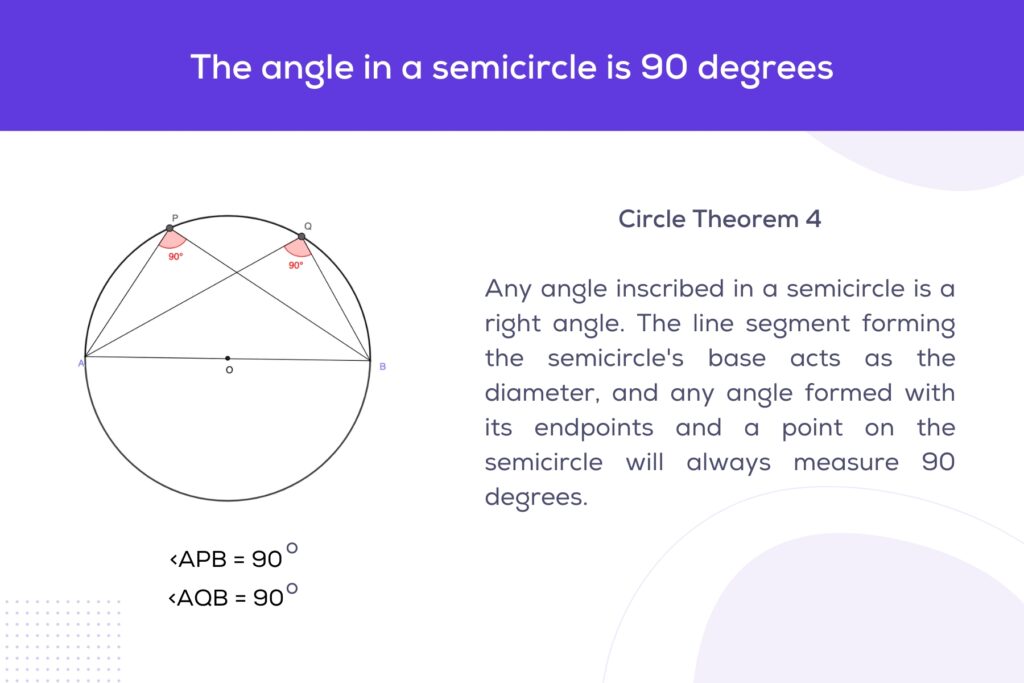
The theorem posits that the angle inscribed in a semicircle is a right angle. That is to say, if an angle is subtended at a point on the circumference of a circle by a diameter of that circle, then the angle is always 90 degrees.

If A, P, and B are points on a circle such that AB is a diameter and P lies on the circumference, then the angle ∠APB inscribed in the semicircle is a right angle.

∠APB=90∘

5. Tangent-Radius Theorem

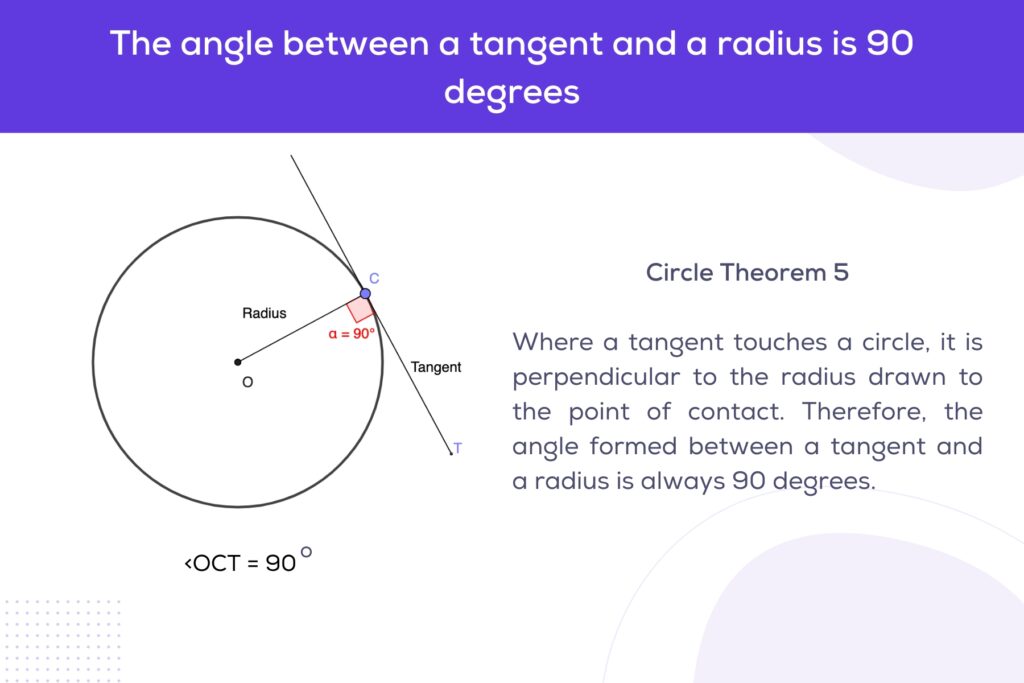
The theorem states that a tangent to a circle is perpendicular to the radius drawn to the point of tangency. In simpler terms, the angle formed between a tangent line and a radius at the point where the tangent meets the circle is always a right angle (90 degrees).

If ST is a tangent to a circle at point C, and OC is the radius drawn to the point of tangency C, then the theorem can be mathematically expressed as:

∠OCT=90∘

6. Two Tangents from a Point Theorem

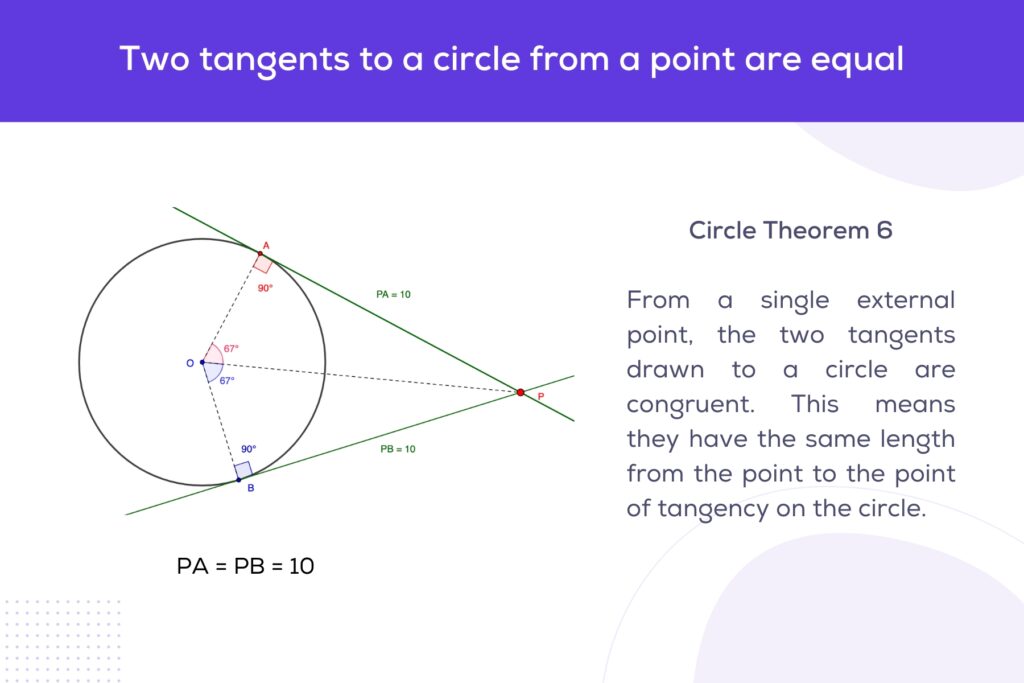
This theorem asserts that if two tangents are drawn to a circle from a single external point, then these two tangents are equal in length. Additionally, the line segment from the external point to the circle’s centre bisects the angle formed between the two tangents.

If PA and PB are two tangents to a circle from an external point P, and O is the centre of the circle, then the theorem can be mathematically stated as:

PA=PB

Moreover, if OP is the line segment from the external point to the circle’s centre, then:

∠APB=2×∠AOB

7. Chord Bisects Diameter

The theorem posits that if a chord is perpendicular to a diameter of a circle at its midpoint, then it bisects the diameter, and conversely, if a chord bisects a diameter, then it must be perpendicular to that diameter.

So, If BC is perpendicular to OD, then: BD=DC and OD bisects BC.

8. Alternate Segment Theorem

This theorem states that the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment of the circle. The alternate segment is defined by the chord and the arc opposite to the point of contact of the tangent.

∠B=∠D

Self Testing – Circle Theorems

1. In a circle, an angle at the circumference subtended by an arc is 35∘. What is the measure of the angle at the centre subtended by the same arc? A) 17.5∘ B) 35∘ C) 70∘ D) 140∘

C) 70∘
According to the Angle at the Centre Theorem, the angle at the centre is twice the angle at the circumference. Therefore, if the angle at the circumference is 35∘, the angle at the centre is 2×35∘=70∘.

2. A triangle is inscribed in a semicircle with one of its sides as the diameter. If the diameter is 10 cm, what is the measure of the angle opposite this side? A) 30∘ B) 45∘ C) 60∘ D) 90∘

D) 90∘
The Angle in a Semicircle Theorem states that an angle inscribed in a semicircle is a right angle. Therefore, the angle opposite the diameter is 90∘.

3. In a circle, two angles are subtended by the same arc and are 45∘ and x∘ respectively. What is the value of x? A) 22.5∘ B) 45∘ C) 60∘ D) 90∘

B) 45∘

The Angles in the Same Segment Theorem tells us that angles in the same segment are equal. Therefore, x=45∘

4. In a circle, a tangent forms an angle of 30∘ with a chord. What is the angle between the chord and the radius at the point of contact? A) 30∘ B) 60∘ C) 90∘ D) 120∘

C) 90∘

The angle between a tangent and a chord is equal to the angle in the alternate segment. However, the angle between a chord and the radius at the point of contact is always 90∘ according to the Tangent-Radius Theorem.

5. In a cyclic quadrilateral, one of the angles is 70∘70∘. What is the measure of its opposite angle? A) 70∘ B) 110∘ C) 130∘ D) 180∘

B) 110∘

The Cyclic Quadrilateral Theorem states that the sum of the opposite angles of a cyclic quadrilateral is 180∘. So, the opposite angle is 180∘−70∘=110∘

6. A chord is 6 cm long and bisects the diameter of a circle. If the radius of the circle is 5 cm, what is the length of each segment of the diameter? A) 2.5 cm B) 5 cm C) 7.5 cm D) 10 cm

B) 55 cm

If a chord bisects the diameter, it divides the diameter into two equal segments. The radius being 5 cm means each segment of the diameter is also 5 cm.

7. In a circle, two chords of equal length subtend angles of x∘ and 40∘ at the center. What is the value of x? A) 20∘ B) 40∘ C) 60∘ D) 80∘

B) 40∘

According to the Equal Chords, Equal Angles Theorem, equal chords subtend equal angles at the center. Therefore, x=40∘.

8. If a tangent is drawn to a circle of radius 4 cm, what is the angle formed between the radius and the tangent? A) 30∘ B) 45∘ C) 60∘ D) 90∘

D) 90∘

The Tangent-Radius Theorem states that the angle between a tangent to a circle and the radius drawn to the point of tangency is always 90∘.

9. Two tangents are drawn from a point P to a circle, touching the circle at A and B. If PA=7 cm, what is the length of PB? A) 3.5 cm B) 7 cm C) 14 cm D) 28 cm

B) 7 cm

The Two Tangents from a Point Theorem states that two tangents drawn from the same external point are equal in length. Hence, PB=7 cm.

10. Problem: In a circle, two chords AB and CD intersect at point E. If AE=3 cm, EB=4 cm, and CE=6 cm, what is the length of ED? A) 0.5 cm B) 2 cm C) 4 cm D) 8 cm

B) 22 cm

According to the Chord Distances Theorem, AE×EB=CE×ED. Therefore, 3×4=6×ED. Solving this gives ED=2 cm.