A-level Maths – Everything You Need to Know

Mastering A-level Maths, known for its complexity and rigorous demands, is essential for students seeking academic success. This guide provides essential strategies, resources, and support to help both students and parents navigate the challenges of A-level Maths effectively. Discover how to approach this demanding subject and unlock a world of opportunities through effective revision techniques and exam preparation

A-level Exams – An Overview

A-levels, represent an integral part of the UK education system and form the bridge between GCSEs and university studies. The in-depth knowledge that A-level subjects provide equips students with the expertise they need to excel in their chosen field of study in higher education.

When it comes to A-level Maths, its significance cannot be overstated. As a subject, it underpins many disciplines such as Engineering, Physics, Computer Science, Economics, and even some branches of Social Sciences. Therefore, a solid grasp of A-level Maths can open doors to a wide range of university courses and subsequent careers.

An A-level Maths course is typically studied over two years. In the first year, students undertake AS (Advanced Subsidiary) level studies, followed by the A2 level in their second year. The content at each level becomes progressively more complex, building on the foundational knowledge gained at the GCSE level. This progression equips students with a comprehensive understanding of mathematical concepts and applications, preparing them well for university-level studies and beyond.

A-level Maths Grading Scheme

Here are the A-level grades by years, ranging from 2019-2021:

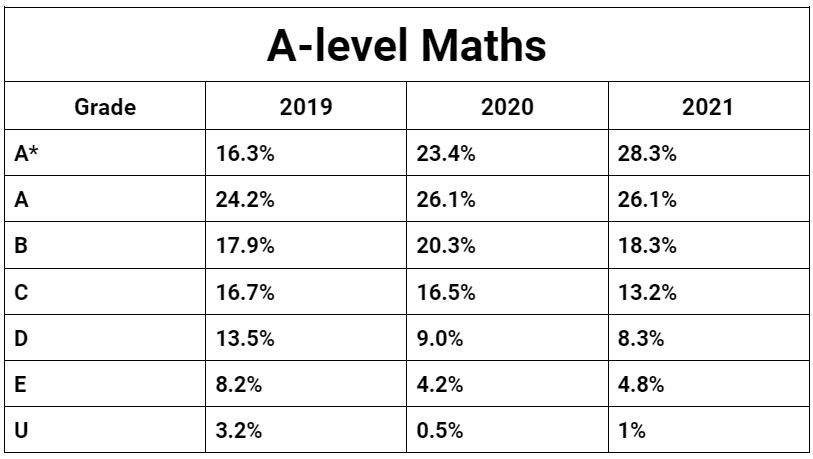
In the A-level system, the grading scale ranges from A* (the highest) to E (the minimum required to pass), with U standing for “ungraded”.

The grades serve as a measure of a student’s understanding of the subject material and their ability to apply this knowledge under exam conditions. In the context of A-level Maths, achieving a high grade often demands not only a solid grasp of mathematical principles, but also problem-solving skills and precision.

These examinations are designed to test students’ abilities across a range of mathematical topics and usually include a mix of question types, such as multiple-choice, short-answer and longer, more complex problems.

The assessment method typically includes three papers:

• Pure Mathematics 1
• Pure Mathematics 2, and
• combined Statistics and Mechanics paper.

The Pure Mathematics papers account for the majority of the final grade, focusing on areas such as algebra, trigonometry, calculus, and sequences and series. The combined Statistics and Mechanics paper evaluates students’ understanding of statistical concepts like data interpretation and probability, along with mechanics topics like forces and motion.

It’s important for students to aim for a consistent performance across all papers to secure a strong overall grade. The final grade is not a simple average of the grades from each paper; instead, it’s calculated based on the total marks across all papers, with certain topics and skills carrying more weight depending on their prominence in the curriculum. Therefore, a holistic understanding of all areas in the curriculum and an ability to apply them effectively are essential for achieving high grades.

A-level Maths – Possible Challanges and How to Tackle Them

Complexity of Problem-Solving

A-level Maths demands a higher level of problem-solving compared to GCSE Maths. Problems are often presented in a way that requires students to combine knowledge from different topics to find a solution. This integrative approach can be a challenge for some students. The only real way to deal with this is practice, take time with your A-level revision and you will see results

Time Management

With the wide range of topics covered in A-level Maths, managing study time effectively can be a challenge for students. The extensive syllabus requires careful planning to ensure that all areas are covered within the revision schedule.

If a student feels like they have difficulty managing their time, we suggest creating study timetables tailored to them and follow it, this is one way to manage the stress that comes with managing time.

Exam Technique

Beyond understanding mathematical concepts, students must also master exam techniques. This includes understanding how to interpret exam questions, demonstrating clear workings, and managing time under exam conditions. Struggles with these techniques can prevent students from achieving their full potential, even when they understand the subject matter.

Transition from GCSE

The leap from GCSE to A-level Maths can be steep for many students. The increased complexity and depth of topics, combined with greater expectations around independent study, can initially be overwhelming.

Recognising these challenges is the first step to overcoming them. As we progress through this guide, we will discuss strategies and resources that can help students navigate these common difficulties, and provide insights for parents on how best to offer support.

Sample A-level Maths Exam Questions and Analysis

Let’s delve into some moderately difficult questions that cover multiple topics in the A-level Maths curriculum. For each question, we’ll provide a detailed solution, as well as highlight common mistakes students often make.

Question 1:

Solve the differential equation:

(dy/dx) = (2y + 3)/(2x - 1)

Solution to Question 1:

This is a first-order linear differential equation and can be solved using an integrating factor.

The common mistake: Students sometimes forget the method or confuse it with other methods for solving differential equations.

Question 2:

Given the sequence 3, 5, 9, 15… which is defined by the nth term u_n = 2n + 1, find the sum of the first 100 terms.

Solution to Question 2:

This is an arithmetic sequence, and the sum can be found using the formula S_n = n/2 * (2a + (n - 1)d). Substituting n = 100, a = 3, and d = 2 gives S_100 = 10100.

The common mistake: Students often confuse the formulae for arithmetic and geometric sequences.

Question 3:

The equation of a curve is y = 2x^3 - 3x^2 - 12x + 20. Find the set of values of x for which y is decreasing.

Solution to Question 3:

To find where the function is decreasing, we need to find its derivative and identify the intervals where it’s negative. The derivative is y' = 6x^2 - 6x - 12. Setting this equal to zero and solving the resulting quadratic gives x = -1 or x = 2. The function is decreasing for x < -1 and x > 2.

The common mistake: Students often forget that the function is decreasing where the derivative is negative, and increasing where the derivative is positive.

Question 4:

If z = 2 + 3i and w = 1 - i, find the value of (z - w)/(zw*), where w* is the complex conjugate of w.

Solution to Question 4:

First find z - w = 1 + 4i and zw* = (2 + 3i)(1 + i) = -1 + 5i. Then (z - w)/(zw*) = (1 + 4i)/(-1 + 5i). Multiplying top and bottom by the conjugate of the denominator gives (1 + 4i)(-1 - 5i)/((-1)^2 - (5)^2) = -21 - 9i.

The common mistake: Students often forget to multiply both the numerator and denominator by the conjugate of the denominator when dividing complex numbers.

Question 5:

Given that tan(θ) = 3/4 and sin(θ) > 0, find the exact value of cos(2θ).

Solution to Question 5:

Since tan(θ) = 3/4 and sin(θ) > 0, we know that θ is in the first quadrant. We can find cos(θ) using the identity cos²(θ) = 1 - sin²(θ), giving cos(θ) = 4/5. Then cos(2θ) = 2cos²(θ) - 1 = 2*(4/5)² - 1 = 7/25.

The common mistake: Students sometimes mistakenly use the wrong quadrant for θ or the incorrect double angle formula.

Not Let’s Move on to More Challenging Questions

In this section, we’ll tackle five more complex questions, which students often find challenging. As before, we’ll provide detailed solutions and highlight common pitfalls.

Question 1:

Solve the differential equation:

(d^2y/dx^2) + 2(dy/dx) - 8 = 0, given that when x = 0, y = 1 and dy/dx = 2.

Solution to Question 1:

This is a second order linear differential equation with constant coefficients. The characteristic equation is r^2 + 2r - 8 = 0, solving for r gives r = -4, 2. The general solution is y = Ae^(-4x) + Be^(2x). Applying the initial conditions to solve for A and B results in A = 1/3, B = 2/3.

The common mistake: Students often struggle with finding the roots of the characteristic equation and applying the initial conditions correctly.

Question 2:

A function is defined by f(x) = ln(x) - x, for x > 0. Prove that the function is always decreasing.

Solution to Question 2:

The derivative of the function is f'(x) = 1/x - 1. For x > 1, f'(x) < 0 and for 0 < x < 1, f'(x) > 0. Hence, f(x) is decreasing for all x > 0.

The common mistake: Students often forget to consider all possible intervals for x when determining whether a function is increasing or decreasing.

Question 3:

If z and w are complex numbers such that |z + w| = |z - w|, prove that z and w are collinear with the origin.

Solution to Question 3:

The fact that |z + w| = |z - w| implies that z and w are equidistant from the origin. This is only possible if z, w, and the origin are collinear.

The common mistake: Students may forget about geometric interpretations of complex number relationships, focusing instead on algebraic manipulations.

Question 4:

The sequence defined by u_n = 2u_(n-1) - u_(n-2), for n > 2, and u_1 = 1, u_2 = 3, is proved to be arithmetic. Find u_100.

Solution to Question 4:

The sequence is indeed arithmetic with d = 2. The first term u_1 = 1, so u_100 = a + 99d = 1 + 99*2 = 199.

The common mistake: Students often get confused between arithmetic and geometric sequences, and may fail to identify the correct difference or ratio.

Question 5:

The parametric equations of a curve are given by x = t^2 - 2t - 8 and y = t^2 + 2t - 1. Find the points on the curve where the tangents are parallel to the x-axis.

Solution to Question 5:

The tangents are parallel to the x-axis when dy/dx = 0. We can find dx/dt and dy/dt separately, then use the formula dy/dx = (dy/dt)/(dx/dt) to find where dy/dx = 0. Solving for t gives t = -1, 1, which correspond to the points (-7, 2) and (-1, 0) on the curve.

The common mistake: Students may struggle with the concept of parametric differentiation and how to apply it to find tangents.

A-Level Maths Marking Scheme

Understanding the A-Level Maths marking scheme can be a vital tool in a student’s arsenal, providing insight into how answers are evaluated and where marks can be gained or lost. Here’s an overview of how it works:

Method marks (M):

These are awarded for knowing and applying the correct method to solve a problem. For instance, using the correct formula or theorem, setting up an equation correctly, or applying a correct differentiation or integration technique. Often, even if the final answer is incorrect, students can still gain method marks if their working shows that they understood the concept or process.

Accuracy marks (A):

These are awarded for obtaining the correct answer, assuming the correct method has been used. To secure accuracy marks, careful calculation is required to avoid mistakes.

Independent marks (B):

These are given for statements or answers that don’t rely on a correct response to a previous part of the question. For example, stating a definition or property, drawing a correct graph, or solving a standalone problem within a larger question.

Dependent marks (D):

These are awarded for answers that rely on a previous part of the question. If an error is made in the previous part but the correct method is applied thereafter, an error carried forward (ECF) policy is usually in place. This means the student could still earn these marks despite the initial mistake.

Remember, full marks are often given for correct answers without working, except where the question specifies otherwise (such as in ‘show that’ questions). However, it’s generally good practice to show working, as it can earn method marks and makes it easier for the examiner to award ECF marks if necessary.

The common mistake: Students often lose marks by not showing their workings out or by making careless errors. It’s important to write clearly, set out calculations logically, and check answers thoroughly.

Revision Resources for A-Level Maths

There are many resources available to help students excel in their A-Level Maths revision. These resources cater to various learning styles and preferences, ensuring each student can find something that suits them. Here are a few of the most effective:

Textbooks

1. Edexcel A Level Mathematics Student Book Year 1 and AS – This book covers all the topics in the curriculum and includes several practice problems with detailed solutions.
2. Cambridge International AS & A Level Mathematics – This book is renowned for its clear explanations and wide variety of questions for practice.

Websites

1. ExamSolutions – A free website that offers detailed video tutorials for all topics covered in the A-level Maths syllabus.
2. Physics and Maths Tutor – This site provides past papers, solution guides, and revision notes.

Online platforms

1. Khan Academy – While not specifically tailored to the A-level syllabus, Khan Academy offers a wealth of resources for all the key Maths topics, and can be an excellent supplementary resource.
2. Integral Maths – A subscription-based service that offers comprehensive resources for A-level Maths.

Revision Apps

1. Gojimo -This free revision app includes A-level Maths quizzes and flashcards to help students test their knowledge and identify areas for improvement.
2. Quizlet – This is an excellent tool for creating custom flashcards to aid memory retention of key formulas and concepts.

Remember, while these resources are useful, they should supplement, not replace, regular coursework and study. It’s also essential to regularly review past papers, as they provide invaluable insight into the exam format and types of questions that are likely to come up.

The common mistake: Many students tend to focus solely on one type of resource or neglect to apply their knowledge by practicing past papers. A balanced approach, including a mix of resources and plenty of practice, tends to yield the best results. Here you can find an extensive collection of A-level maths past papers.

The Benefits of A-Level Maths Tuition

Personalised tuition can be particularly beneficial for A-Level Maths due to the subject’s complexity and the individualised understanding students often need to fully grasp concepts

One-to-one attention

Maths is a subject where one small misunderstanding can lead to significant gaps in knowledge. An A-level maths tutor can provide personalised, one-on-one attention, ensuring that the student’s unique learning needs are met, and all their questions are answered. Tutors can also identify and resolve any gaps in foundational knowledge, enabling the student to tackle advanced topics confidently.

Subject-Specific Expertise

A dedicated Maths tutor possesses subject-specific expertise that goes beyond what a general tutor can provide. This expertise allows them to explain complex concepts in simple terms, provide insights into the marking scheme, and advise on effective exam strategies specific to A-Level Maths.

Customised Learning Pace

Not all students learn at the same pace. A tutor can adjust the pace of teaching to match the student’s learning speed, ensuring they fully understand a topic before moving on to the next one. This customised pace can be especially beneficial for complex A-Level Maths topics.

Flexibility with Online Tuition

Online tuition provides flexibility that traditional in-person tuition often can’t match. Lessons can be conducted from anywhere, fitting around the student’s schedule. Online tuition can also provide access to a wider pool of tutors, ensuring the student finds the one that best suits their learning style and needs.

Boosting Confidence

A tutor can boost a student’s confidence in Maths by reinforcing their understanding of the subject and helping them overcome any challenges they may be facing. Increased confidence often leads to improved performance in exams.

Remember, while A-Level Maths tuition can provide these benefits, it’s crucial to find a tutor who is a good match for the student’s learning style and needs.

Conclusion

The journey through A-level Maths, while challenging, is undoubtedly rewarding. It offers an opportunity to delve deeper into the fascinating world of numbers, fostering critical thinking, problem-solving skills, and a more profound understanding of the mathematical principles that underpin our universe.

It’s important to remember that every student’s journey is unique. The support they need may vary – some may find their path unimpeded, while others may stumble upon obstacles that seem insurmountable. Here’s where personalised tutoring comes into play. It’s not a sign of weakness but an intelligent strategy for success. Even high achievers can significantly benefit from the tailored guidance a tutor provides. Learning from someone who has successfully navigated the path you’re treading can be incredibly advantageous.