in GCSE Chemistry, understanding relative atomic mass is essential for grasping how elements combine and interact in chemical reactions. Relative atomic mass, often represented as Ar, provides a way to compare the average mass of atoms in elements and is key to understanding chemical quantities and stoichiometry. Every student needs to know how to calculate relative atomic mass because mastering this concept not only supports success in exams but also builds a foundation for more advanced chemistry topics.
In this blog, we aim to offer a comprehensive guide to calculating relative atomic mass, covering definitions, calculations, and explanations of concepts like abundance and mass number. By the end, you’ll be equipped to confidently calculate relative atomic mass, a vital skill in GCSE Chemistry.
What is Relative Atomic Mass?
Relative atomic mass, denoted as RAM or Ar, is the weighted average mass of the atoms of an element, taking into account the masses and abundances of its naturally occurring isotopes. It’s called “relative” because it’s measured against the mass of a carbon-12 atom, which is set at exactly 12. Ar values are not whole numbers, as they account for multiple isotopes and their abundances.
How to Calculate Relative Atomic Mass?
Relative atomic mass is calculated by adding up the masses of all the isotopes of an element, each weighted by its natural abundance. This means each isotope’s mass is multiplied by its percentage abundance, and the results are added together.
Finally, this total is divided by 100 to get an average based on the element’s natural distribution. This calculation provides an estimate of the average mass of an atom for that element, reflecting how it occurs in nature.
Calculating relative atomic mass involves understanding isotopic abundance and mass number. The mass number of an isotope is the sum of its protons and neutrons, while isotopic abundance is the proportion of each isotope found in nature. Here’s what you need to know for proper calculation of relative atomic mass:
Key Terms to Know
- Isotope: Variants of an element with the same number of protons but different numbers of neutrons. This difference in neutrons results in different mass numbers.
- Mass Number: The sum of protons and neutrons in an atom’s nucleus. Each isotope of an element has its own mass number.
- Abundance: The percentage of each isotope that occurs in nature for that element.
What Is A Formula For Relative Atomic Mass?
The relative atomic mass (Ar) of an element with multiple isotopes is calculated using the formula:
Relative Atomic Mass (Ar) = Σ(Mass of Isotope × Abundance) 100
This formula involves multiplying the mass of each isotope by its abundance (expressed as a percentage) and then dividing by 100 to account for the total percentage.
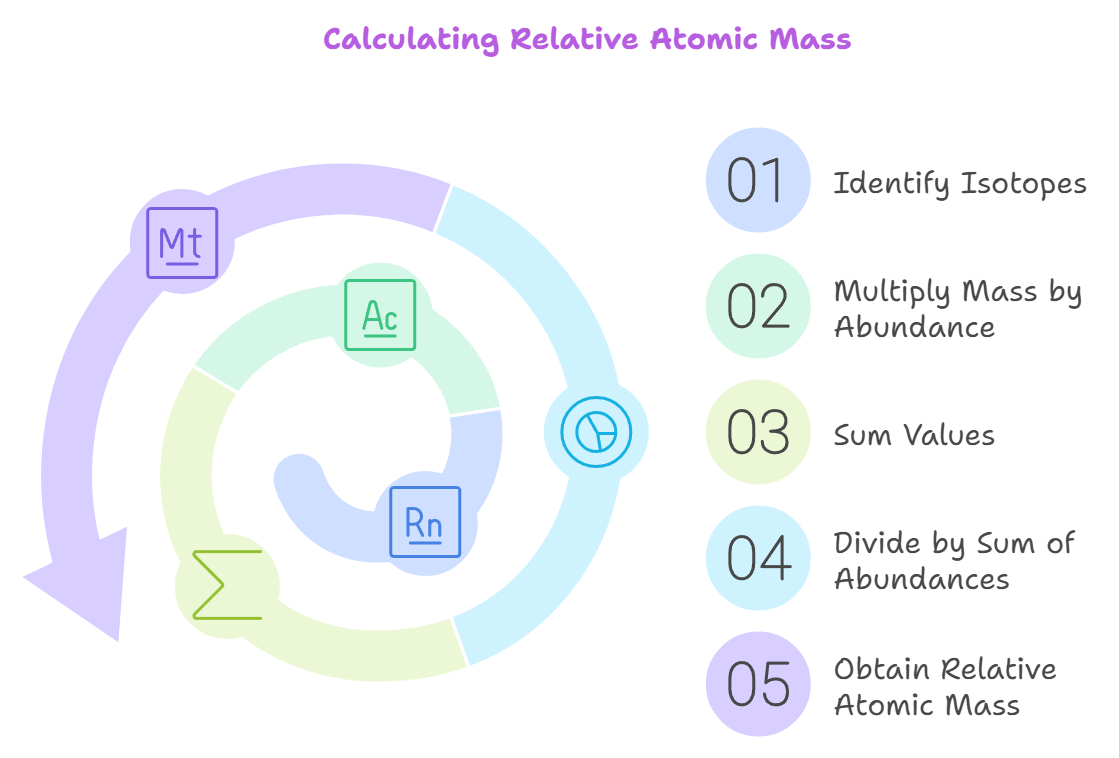
Step-by-Step Guide to Calculate Relative Atomic Mass
After we learn theory of how to calculate relative atomic mass, it’s time to do some practice work. Let’s walk through a worked example to make the process clear.
Example: Calculating the Relative Atomic Mass of Chlorine
Chlorine has two main isotopes:
- Chlorine-35 with a mass of 35 and an abundance of 75%
- Chlorine-37 with a mass of 37 and an abundance of 25%
To find the relative atomic mass of chlorine, we’ll follow these steps:
Step 1: List Each Isotope’s Mass and Abundance
Identify the mass number and natural abundance of each isotope.
- Isotope 1: Chlorine-35
- Mass = 35
- Abundance = 75%
- Isotope 2: Chlorine-37
- Mass = 37
- Abundance = 25%
Step 2: Multiply Each Mass Number by Its Abundance
Multiply the mass number of each isotope by its percentage abundance. This step calculates the contribution of each isotope to the total atomic mass, weighted by its abundance.
35 × 75 = 2625
37 × 25 = 925
Step 3: Add the Results
Add the contributions from each isotope together. This sum represents the combined mass contribution from all isotopes.
2625 + 925 = 3550
Step 4: Divide by 100
Divide the total by 100 to obtain the weighted average, accounting for the fact that the abundances are percentages.
Relative Atomic Mass = 3550 100 = 35.5
Thus, the relative atomic mass of chlorine is 35.5.
Practice Example: Calculating the Relative Atomic Mass of Magnesium
Magnesium has three naturally occurring isotopes:
- Magnesium-24 with a mass of 24 and an abundance of 79%
- Magnesium-25 with a mass of 25 and an abundance of 10%
- Magnesium-26 with a mass of 26 and an abundance of 11%
Multiply Each Mass Number by Its Abundance:
24 × 79 = 1896
25 × 10 = 250
26 × 11 = 286
2. Add the Results:
1896 + 250 + 286 = 2432
3. Divide by 100:
Relative Atomic Mass = 2432 100 = 24.32
The relative atomic mass of magnesium is 24.32.
Why Do We Use This Calculation?
This calculation is essential because elements don’t exist as single, uniform isotopes in nature. By calculating the weighted average, we get an accurate reflection of the element’s mass as it naturally occurs, which is useful in chemical equations, stoichiometry, and other scientific calculations. This relative atomic mass then helps scientists and students predict how elements will behave in reactions.
Why is Relative Atomic Mass Important in Chemistry?
Relative atomic mass is crucial in chemistry because it gives a practical way to work with elements as they naturally occur. Since elements often exist as a mix of isotopes, relative atomic mass represents the weighted average of these isotopes, allowing chemists to predict and calculate the behavior of elements in reactions more accurately.
It’s used in stoichiometry to determine the mass of elements in compounds and reactions, enabling precise measurements when working with chemical formulas. In short, it’s an essential tool for balancing equations, measuring reactants, and understanding how elements interact on an atomic level.
How Does Relative Atomic Mass Differ from Atomic Mass?
Relative atomic mass and atomic mass are related but differ in their focus and usage:
- Relative Atomic Mass (Ar) is a weighted average based on the isotopes of an element and their natural abundance, giving a decimal value that represents how an element typically occurs in nature. It’s dimensionless and used in chemical calculations as an averaged reference.
- Atomic Mass (or Atomic Mass Number) is the specific mass of a single isotope of an element, measured in atomic mass units (amu).
For example, carbon-12 has an atomic mass of exactly 12 amu. Atomic mass reflects the precise mass of individual isotopes, rather than the averaged mix found in nature.
In summary, while atomic mass refers to a single isotope, relative atomic mass is a natural average, essential for practical applications in chemistry.
How Does Relative Atomic Mass Help in Chemical Calculations?
Relative atomic mass simplifies chemical calculations by providing an average mass for each element based on its isotopes and their natural abundances. Here’s how it plays a crucial role:
- Mole Calculations: Relative atomic mass allows chemists to calculate moles, as it represents the mass of one mole (in grams) of an element. For instance, if carbon has a relative atomic mass of 12, then one mole of carbon weighs 12 grams. This makes it easy to convert between grams and moles, essential for quantifying reactants and products in chemical reactions.
- Balancing Chemical Equations: When balancing equations, relative atomic mass helps calculate the mass of each element involved, making it possible to determine exact ratios of reactants and products. For example, if we know the relative atomic masses of hydrogen and oxygen, we can calculate the precise masses needed to form water, ensuring reactions are balanced accurately.
- Determining Empirical and Molecular Formulas: Relative atomic mass enables the calculation of both empirical (simplest ratio) and molecular formulas for compounds. By knowing the mass of each element in a compound, chemists can calculate the simplest formula or the exact molecular formula, which is vital for identifying compounds and predicting their properties.
- Calculating Concentrations in Solutions: In solutions, chemists use relative atomic mass to calculate molarity (moles per litre), allowing them to create solutions with precise concentrations.
- Stoichiometry: In stoichiometry, which involves calculations of reactants and products in chemical reactions, relative atomic mass helps determine the quantities of substances that react or are produced. This allows chemists to predict how much of each substance is needed or generated in a reaction, ensuring efficiency and minimising waste.
In essence, relative atomic mass bridges the atomic scale with measurable lab quantities, making it possible to work with elements and compounds in real-world chemical reactions with precision.
Conclusion
Understanding relative atomic mass is fundamental in GCSE Chemistry, as it links atomic theory with practical applications in chemical calculations. By providing a weighted average of an element’s isotopes, relative atomic mass allows students to calculate moles, balance equations, determine formulas, and understand stoichiometry with precision. This concept not only simplifies the complexities of chemistry but also offers insights into the behavior of elements in natural and experimental contexts.
Mastering how to calculate relative atomic mass equips students with essential tools for success in exams and lays a strong foundation for advanced studies in chemistry. For those seeking extra support, GCSE chemistry tutors can provide personalized guidance, helping students grasp challenging concepts, refine their calculation skills, and prepare effectively for exams. With expert help, students can approach chemistry with confidence and achieve academic success.
FAQs
What are the units of relative atomic mass?
Relative atomic mass is a dimensionless quantity, meaning it has no units. It is a ratio that compares the average mass of an element’s atoms to 1/12th the mass of a carbon-12 atom.
How is relative atomic mass calculated?
Relative atomic mass is calculated by multiplying each isotope’s mass by its natural abundance, adding the results, and dividing by 100. This provides an average mass that reflects the natural mix of isotopes in the element.
How does relative atomic mass differ from atomic mass?
Relative atomic mass is a weighted average based on the isotopes of an element, while atomic mass (or atomic mass number) is the mass of a single isotope, measured in atomic mass units (amu). It represents the element’s natural isotopic composition, whereas atomic mass is specific to individual isotopes.
What is the Relative Molecular Mass?
Relative molecular mass, often represented as Mr, is the sum of the relative atomic masses of all atoms in a molecule. It gives the average mass of a molecule compared to 1/12th the mass of a carbon-12 atom.
