GCSE Maths is one of the mandatory subjects in UK curriculum. Catering to students in Year 10 and Year 11, GCSE Maths exams are structured into two tiers: Foundation and Higher. The Foundation tier covers basic concepts, aimed at grades 1-5, while the Higher tier challenges students with more complex topics, targeting grades 4-9.
In GCSE Maths, students are assessed through a series of papers, each designed to test different areas of mathematical proficiency. Typically, there are three papers – one focusing on non-calculator skills and the other two allowing the use of calculators. The nature of questions varies, ranging from multiple-choice to more complex problem-solving tasks.
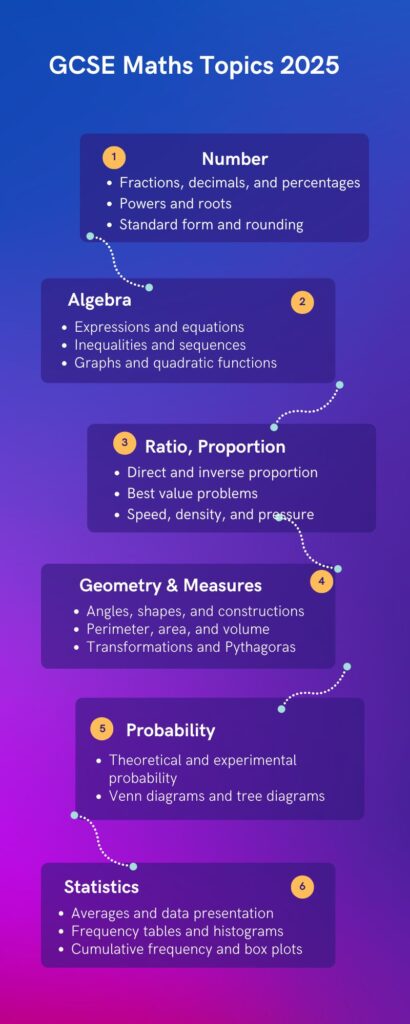
What is studied in GCSE maths?
GCSE Maths covers a broad range of topics designed to develop students’ numerical and problem-solving skills. The curriculum is divided into several key areas:
- Number: This includes operations, fractions, decimals, percentages, powers, roots, and the use of standard form and significant figures.
- Algebra: Topics include simplifying expressions, solving equations and inequalities, formula manipulation, and graphing functions.
- Ratio, Proportion, and Rates of Change: This involves working with ratios, direct and inverse proportion, and problems involving rates of change.
- Geometry and Measures: Students learn about properties of shapes, including angles, perimeter, area, volume, and theorems related to circles. It also covers bearings and scales, transformations, and vectors.
- Probability: This includes the calculation and interpretation of probabilities, including the use of probability trees and other diagrams.
- Statistics: Students work with data collection, data representation through graphs and charts, and measures of central tendency and spread.
GCSE Maths topics
Here’s a table summarising the key differences between foundation and higher tier:
| Topic | Foundation Tier | Higher Tier |
|---|---|---|
| Numbers | Percentages, decimals, fractions, basic operations | Surds, indices, logarithms, complex numbers |
| Algebra | Linear equations, inequalities, simple polynomials | Quadratics, solving equations with multiple unknowns, calculus |
| Geometry | Area, perimeter, volume, Pythagoras’ theorem | Trigonometry, vectors, coordinate geometry |
| Statistics | Mean, median, mode, range | Probability, hypothesis testing, correlation |
Number
The Number topic in GCSE Maths is essential, forming the base for all other mathematical concepts. This topic is typically seen as accessible, though some aspects can present challenges.
Key Concepts
- Basic arithmetic operations: addition, subtraction, multiplication, division.
- Understanding and working with fractions, decimals, and percentages.
- Grasping the concept of powers and roots.
To achieve the highest grade in this area, students need to be more than just proficient in these basic operations. They must also comprehend their practical applications, be adept at solving complex problems, maintain accuracy in calculations, and apply these number concepts in varied contexts. A deep and thorough understanding, which goes beyond mere computation, is key to excelling in this topic.
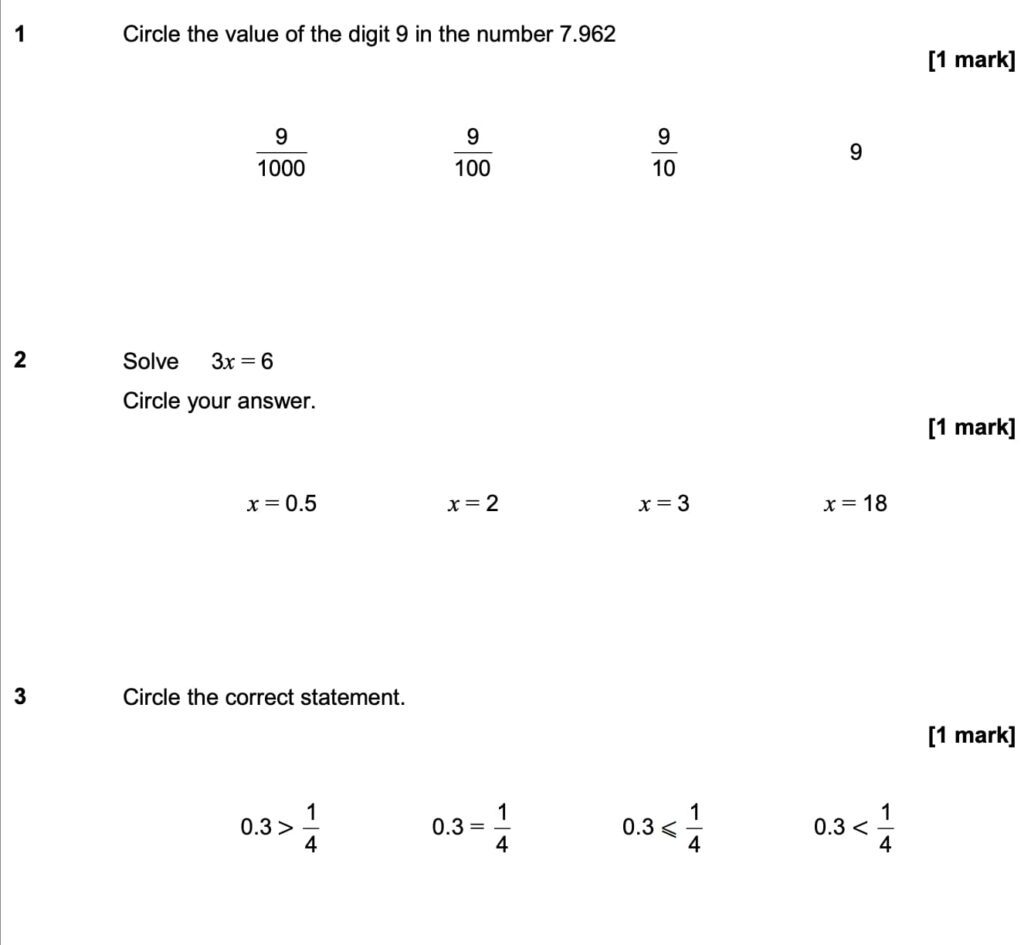
Algebra
Algebra is a vital component of GCSE Maths, introducing students to abstract thinking and problem-solving with unknown variables. It is considered moderately challenging, as it requires a shift from concrete numbers to abstract symbols and expressions.
Key Concepts
- Understanding and manipulating algebraic expressions.
- Solving linear and quadratic equations.
- Working with inequalities, sequences, and algebraic fractions.
For top grades, students must demonstrate a strong grasp of these concepts, an ability to approach problems logically, and apply algebraic methods in various contexts. Mastery in algebra involves not just solving equations but also understanding their real-world applications, constructing arguments, and justifying solutions. A deep conceptual understanding and a strategic approach to problem-solving are crucial for excelling in this area.
Ratio and Proportion
Ratio and Proportion in GCSE Maths involve comparing quantities and understanding their relationship, a crucial skill in both academic and real-life contexts. This topic is generally perceived as moderately challenging due to the abstract nature of ratios and proportional reasoning.
Key Concepts
- Understanding and calculating ratios.
- Solving problems involving direct and inverse proportion.
- Applying these concepts to real-world scenarios, like scale drawings and recipe adjustments.
To excel in exams, students need to be adept at identifying and solving ratio and proportion problems, demonstrate clear and logical reasoning, and apply these concepts in various practical situations. Mastery in this area is not just about computational skills, but also about understanding and interpreting the relationships between different quantities.
Geometry and Measure

Geometry and Measure in GCSE Maths cover a wide range of topics related to shapes, sizes, and the properties of space. This area can be challenging due to its visual and spatial nature, requiring a good understanding of both theoretical and practical aspects.
Key Concepts
- Understanding properties of different shapes.
- Calculating area, volume, and surface area.
- Skills in accurate measurement and conversion between units.
Achieving high marks in this topic requires a solid grasp of these concepts, precision in calculations, and the ability to apply geometrical and measurement principles in various contexts. It’s not just about memorising formulas; it’s about understanding how and why they work in real-world situations.
Probability

Probability in GCSE Maths involves understanding and calculating the likelihood of various events. This topic is often seen as tricky because it requires both logical thinking and an understanding of chance and risk.
Key Concepts
- Basic probability principles and terminology.
- Calculating probabilities in different contexts.
- Understanding and applying concepts of conditional probability and probability trees.
To score top marks, students need to demonstrate clear reasoning, accurate calculation skills, and the ability to apply probability concepts to solve real-world problems. A deep understanding of the underlying principles of probability is essential for excelling in this area.
Statistics
Statistics in GCSE Maths is about collecting, analysing, interpreting, and presenting data. It’s a moderately challenging area that combines mathematical skills with real-world relevance.
Key Concepts
- Data collection and sampling methods.
- Representing data through graphs and charts.
- Understanding and calculating measures of central tendency and spread.
Excellence in statistics requires not only the ability to calculate and analyse data but also to interpret and present findings in a meaningful way. A high level of analytical thinking and precision is needed to excel in this topic.
What GCSE maths papers are there?
GCSE Maths typically consists of three papers that students must sit as part of their assessment:
Paper 1: Non-Calculator
This paper tests students’ ability to perform calculations and solve mathematical problems without the use of a calculator. It covers all areas of the syllabus and is designed to assess understanding and fluency with numerical and algebraic concepts.
Paper 2: Calculator
This paper allows the use of a calculator and tests students on the same range of topics as Paper 1, but with problems that are generally more suitable for calculator use. This may include more complex calculations, statistical data interpretation, and problems involving geometric measurements.
Paper 3: Calculator
Similar to Paper 2, this paper also requires the use of a calculator. It typically includes a range of questions that test the breadth and depth of students’ mathematical knowledge and application skills.
All three papers usually cover the following key areas: Number, Algebra, Ratio, Proportion and Rates of Change, Geometry and Measures, Probability, and Statistics. The distribution of questions across these topics can vary, but each paper is structured to assess a comprehensive understanding of the curriculum.
The exam format can differ slightly between different examination boards in the UK, such as AQA, Edexcel, OCR, and others, but the fundamental structure of three papers is common. Each paper is typically weighted equally in contributing to the final grade.
To get familiar with the structure and question styles, it’s highly recommended that students practise using GCSE Maths past papers provided by their specific exam board. These are invaluable for building confidence and improving exam technique.
Conclusion
In conclusion, mastering GCSE Maths topics 2025 requires dedication, practice, and a deep understanding of various topics like Number, Algebra, Ratio and Proportion, Geometry and Measure, Probability, and Statistics. Each area has its unique challenges and learning requirements, but with the right approach and tools, excelling in GCSE Maths is certainly achievable. For those seeking additional support, online GCSE Maths tutoring can be an invaluable resource. providing personalised guidance to help students understand complex concepts, improve their problem-solving skills, and achieve their academic goals.
Ready to Boost Your GCSE Maths Grade?
Don’t let tricky topics hold you back—get the support you need to succeed. With tailored online GCSE Maths tutoring from expert tutors, you can build confidence, sharpen your skills, and tackle even the toughest exam questions. Book your free trial today and take the first step towards exam success!
FAQs:
how many topics are there in gcse maths?
There are six main topics in GCSE Maths. These are:
- Number
- Algebra
- Ratio, Proportion and Rates of Change
- Geometry and Measures
- Probability
- Statistics
Each topic is assessed across both Foundation and Higher tiers, with varying levels of difficulty.
How to get grade 9 in GCSE maths?
To achieve a grade 9 in GCSE Maths, focus on mastering the entire syllabus with particular attention to higher-level topics. Practice extensively with past papers and challenging questions to hone problem-solving skills. Regularly review mistakes to improve understanding and seek help from teachers or tutors when needed. Stay consistent and disciplined in your studies to excel in the exam
What topics are in calculator GCSE Maths?
The calculator paper covers all GCSE Maths topics, including:
- Number
- Algebra
- Ratio, proportion and rates of change
- Geometry and measures
- Probability
- Statistics
You may be required to solve more complex problems involving trigonometry, simultaneous equations, or compound measures that are easier to manage with a calculator.
What topics are in non calculator GCSE Maths?
However, questions are designed to be solvable without a calculator, often focusing more on arithmetic, estimation, fractions, and simplifying expressions.
The non calculator paper also includes all main topics:
- Number
- Algebra
- Ratio, proportion and rates of change
- Geometry and measures
- Probability
- Statistics
Which GCSE maths paper is the easiest?
There is no official answer to which paper is the easiest, as it depends on each student’s strengths. However, many students find Paper 1 (Non-Calculator) easier because it often focuses more on number skills and mental arithmetic.
Others may prefer Paper 2 and Paper 3 (Calculator) since they can use a calculator to handle more complex calculations. The difficulty can vary depending on the exam board and the specific questions each year. Practising all papers is the best way to build confidence and spot which suits you best.
What topics will be in GCSE Maths 2025?
GCSE Maths 2025 will continue to assess the full range of topics outlined in the national curriculum:
- Number
- Algebra
- Ratio, proportion and rates of change
- Geometry and measures
- Probability
- Statistics
Any specific changes will be published by exam boards like AQA, Edexcel, or OCR. It’s best to check their official websites for the most up-to-date information.