Force Equations Made Easy: Key Formulas for GCSE Physics
In fact, force equations are an essential part of understanding how things move and interact in physics. So, if you’ve ever wondered how objects change speed, direction, or position, force is at the heart of it all. For students tackling force equations GCSE physics, knowing how to apply these equations is key to solving many problems.
To start with, force is what makes something move or stop. It’s any push or pull on an object, and it affects how that object behaves. By using the force formula, we can calculate how much force it takes to move or accelerate something. Although, it might sound complicated at first, once you understand the basics, it becomes much easier to handle.
This blog will help you break down the different force equations you’ll encounter in physics, from the Newton force formula to the centripetal force equations. Moreover, we’ll explain what each equation means and show you how to use them to solve real problems. Whether you’re studying for a physics exam or just curious, we’re here to make it easy and clear!

What is Force?
To begin with, force is a key concept in physics. It’s a push or pull on an object that causes it to move, stop, or change direction. In simple terms, force causes a change in motion. The SI unit of force is the Newton (N), named after Sir Isaac Newton, who developed the basic principles of force in physics.
For example, forces are what make things happen-whether it’s a ball thrown in the air or a car speeding on the road. Forces can act in different directions, and their effect depends on their size, direction, and where they are applied.
But, there is a common misconception that force only acts on moving objects. In fact, force can also act on stationary objects, causing them to move or change shape. Another misunderstanding is that force is just about pushing or pulling. However, force also includes gravity, friction, and tension, all of which affect motion in different ways.
Exploring Fundamental Force Equations in Physics
In the first place, force is central to many physical phenomena, and understanding key force equations will help you solve problems and understand how the world works. Below, we’ll explore some of the most important force equations and their applications.
Newton’s Second Law of Motion
Equation: F = m × a (Force equals Mass multiplied by Acceleration)
- Explanation: This equation tells us how force, mass, and acceleration are connected. If you apply a greater force to an object, it will accelerate more-if the mass stays the same. Likewise, if you have a larger mass, the acceleration will be less for the same force.
- Applications: Think about pushing a car. If the car is small and light, you can push it with less force to get it moving. A bigger, heavier car would require more force to move at the same speed.
Force Equations: Gravitational Force
Equation: F = G × (m₁ × m₂) / r² (Gravitational Force between two objects)
- Explanation: This equation explains how the gravitational force between two objects is calculated. Here, G is the gravitational constant, m₁ and m₂ are the masses of the objects, and r is the distance between them. The force decreases with distance-this is why objects farther apart exert less force on each other.
- Real-life Examples: Earth’s gravity is a perfect example. It’s why objects fall to the ground, and why the Earth pulls on us and everything else around it.
Force Equations: Electromagnetic Force
Equation: F = k × (q₁ × q₂) / r² (Electromagnetic Force between two electric charges)
- Explanation: This equation tells us the force between two electric charges. It’s similar to the gravitational force equation, but for electric charges. The constant ‘k’ helps calculate the strength of the force based on the charges and the distance between them.
- Application: Think about static electricity. When you rub a balloon on your hair, it becomes charged and can attract or repel objects, depending on the charges.
Force Equations: Frictional Force
Equation: F = μ × N (Frictional force between two surfaces)
- Explanation: Friction is the force that resists the motion of two surfaces sliding against each other. The coefficient of friction (μ) is a number that tells you how rough or smooth the surfaces are. N is the normal force, which is the force pushing the two surfaces together (for instance, gravity pulling an object down on a table).
- Real-world Application: When you push a heavy box, it’s hard to move because of friction. Likewise, on a slippery road, the friction between the tires and the surface is reduced, which is why cars can skid.
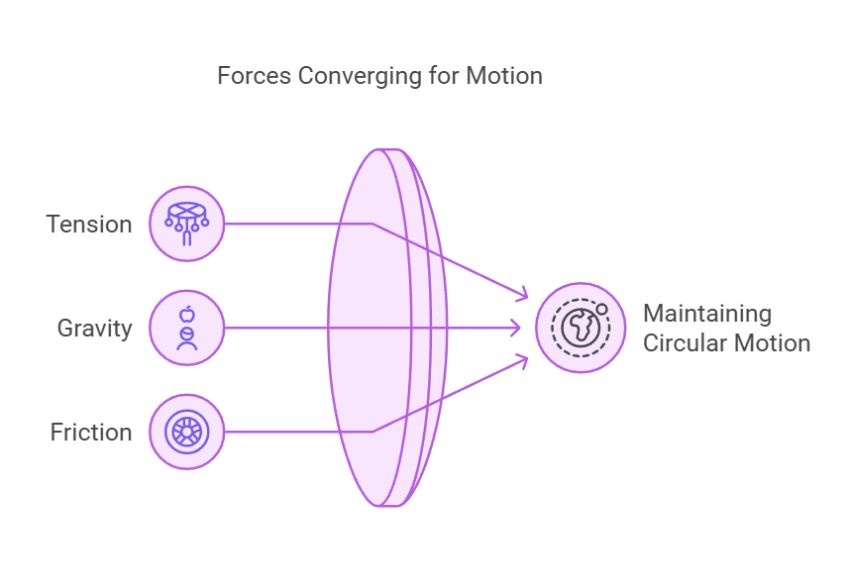
Force Equations: Centripetal Force
Equation: F = (m × v²) / r (Centripetal force required to keep an object moving in a circular path)
- Explanation: This equation calculates the force needed to keep an object moving in a circular path. As the object moves faster, the required force increases. The mass of the object and the radius of the circle also affect the force needed.
- Examples: This is the force that keeps satellites in orbit or keeps a car from sliding off a curve. It’s the reason why the cars on a race track have to slow down when they turn sharply.

Practical Applications of Force Equations in Everyday Life
In fact, force equations play a crucial role in many aspects of our daily lives. From engineering to sports and astronomy, these equations help us understand and predict how objects move and interact. Let’s explore how force equations are applied in different fields.
Engineering: How Force Equations Help Engineers Design Structures and Vehicles
In engineering, force equations are essential for designing buildings, bridges, and vehicles. By using force formulas, engineers calculate the forces that objects will experience, such as weight, pressure, and friction. These calculations ensure that structures can withstand external forces, like wind or traffic, without collapsing.
For example, the Newton force formula is used to determine how much force is needed to move a car or lift a heavy load.
Sports: Application of Force in Sports like Football or Cycling
In sports, force is everywhere. Whether it’s the force needed to kick a football or the friction between bicycle tires and the road, force equations help athletes optimise their performance. For example, in football, players apply force to the ball to make it move, and in cycling, the friction between the tires and the ground is key to maintaining control and speed. Force equations GCSE physics helps students understand these real-world applications, making learning fun and relevant.
Astronomy: Role of Gravitational Force in Space Exploration and Satellite Orbits
In astronomy, force equations are vital for understanding the movement of celestial bodies. The gravitational force equation plays a key role in calculating the forces between planets, stars, and satellites.
For instance, when launching satellites into orbit, engineers use the gravitational force equation to determine the necessary velocity to keep the satellite in a stable orbit. Centripetal force equations are also used to describe the forces that keep planets revolving around the sun.
Thus, by understanding and applying these force equations, we can solve real-world problems, enhance our knowledge in various fields, and see how physics impacts our daily lives.
Mastering Force Equations for Problem Solving
Force equations are powerful tools for solving physics problems, and once you get the hang of them, they become much easier to use. Here’s a simple step-by-step guide on how to apply force equations effectively.
Step-by-Step Guide
Let’s say you’re asked to calculate the force required to accelerate a car. Using Newton’s Second Law of Motion, which states:
F = ma (Force = Mass × Acceleration)
you can easily find the force if you know the car’s mass and its acceleration. For example, if the car has a mass of 1,000 kg and it accelerates at 2 m/s², the force required is:
F = 1,000 kg × 2 m/s² = 2,000
Tips for Students
To improve your understanding and problem-solving skills, follow these tips:
- Break down the problem: Identify which force equation applies to the scenario.
- Write down known values: Make sure you have all the information you need (mass, acceleration, etc.).
- Substitute and calculate: Plug the known values into the equation and solve.
- Practice regularly: The more you practice, the easier it becomes to apply force equations to various problems.
By following these steps and practicing, you can become more confident in solving problems using force equations. It’s all about breaking things down into manageable steps and applying the right formula at the right time.
Force Equations: Connecting Physics to Real-World Applications
Therefore, understanding force equations is crucial because they help us explain and predict how objects behave. In our daily lives, we use these equations in various real-world situations, from the way cars move to how machines operate. By understanding the relationship between forces and motion, we can design better systems and improve everyday experiences.
Real-World Relevance
Firstly, force equations help us understand how things like cars, planes, and even sports equipment work. For example, when driving a car, you’re dealing with force and acceleration. Understanding how force works helps us use that knowledge in designing vehicles or other machinery to function efficiently.
Impact on Technology and Innovation
Secondly, force equations are foundational in fields like engineering and technology. From the development of rockets to creating efficient engines, knowing how to calculate force allows us to innovate and improve technologies. These equations are used in everything from centripetal force in space travel to vehicle safety designs.
Benefits for Students
Lastly, learning force equations helps students build important problem-solving skills. Understanding these concepts not only prepares students for exams like force equations GCSE physics but also boosts their critical thinking and analytical abilities.

How to Avoid Mistakes When Using Force Equations
When using force equations, it’s easy to make mistakes that can lead to incorrect results. Let’s got through the common errors and offer simple tips to help you avoid them, ensuring accurate calculations every time.
Wrong units
A common mistake in force equations is using the wrong units. Make sure to use the correct ones: mass in kilograms (kg), acceleration in meters per second squared (m/s²), and force in newtons (N). Mixing up units can lead to wrong results.
Misinterpreting Force Component
Another mistake is misunderstanding the different forces. For example, gravity pulls objects down, while friction resists movement. Mixing them up or forgetting to consider both can cause errors.
Not Considering All Forces
Keep in mind, to always include all the forces acting on an object. If you only think about gravity and ignore others like friction or air resistance, the result may be wrong. Consider all forces to get the correct answer.
Conclusion
As discussed, Force equations are essential for understanding how things work in the world around us. From Newton’s second law to centripetal force, these formulas are fundamental to physics. They help solve real-world problems and improve your critical thinking skills.
Plus, remember, learning force equations takes practice. Keep working through problems, and don’t hesitate to explore more about force formula physics. Whether you’re studying for GCSE physics or looking to expand your knowledge, continual learning is key to mastering these concepts.
Also, if you’re struggling with force equations or physics in general, consider seeking extra help from Physics online tutors. As, they offer personalised guidance, simplify complex topics, and help you succeed in studies and real-life. Keep practicing and stay curious-you’ll soon use force equations with confidence!
FAQs:
What are the 3 formulas for force?
Newton’s Second Law of Motion: F = m ⋅ a (Force = Mass × Acceleration)
Gravitational Force: F = G ⋅ (m₁ ⋅ m₂) / r² (Force between two objects due to gravity)
Frictional Force: F = μ ⋅ N (Force due to friction between two surfaces)
What are the two equations for force?
Newton’s Second Law: F = m ⋅ a (Force = Mass × Acceleration)
Gravitational Force: F = G ⋅ (m₁ ⋅ m₂) / r² (Force between two objects due to gravity)
What is Newton's Second Law of Motion?
Newton’s Second Law states that the force acting on an object is equal to the mass of that object multiplied by its acceleration. This is expressed as F = m ⋅ a.
How Do You Calculate Frictional Force?
Frictional force is calculated using the formula F = μ ⋅ N, where μ is the coefficient of friction, and N is the normal force (the force perpendicular to the surface).
What is the 3rd law of forces?
Newton’s Third Law states that for every action, there is an equal and opposite reaction. This means that forces always come in pairs.
What are non-contact forces?
Non-contact forces are forces that act on objects without physical contact. For example: gravitational force, magnetic force, and electrostatic force.